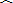题目内容
如图.已知A、B两点的坐标分别为A(0,2
),B(2,0).直线AB与反比例 函数y=
函数y=
的图象交于点C和点D(-1,a).
(1)求直线AB和反比例函数的解析式.
(2)求∠ACO的度数.
(3)将△OBC绕点O逆时针方向旋转α角(α为锐角),得到△OB′C′,当α为多少时,OC′⊥AB,并求此时线段AB’的长.
| 3 |
 函数y=
函数y=| m |
| x |
(1)求直线AB和反比例函数的解析式.
(2)求∠ACO的度数.
(3)将△OBC绕点O逆时针方向旋转α角(α为锐角),得到△OB′C′,当α为多少时,OC′⊥AB,并求此时线段AB’的长.
(1)设直线AB的解析式为:y=kx+b,
把A(0,2
),B(2,0)分别代入,得
,解得k=-
,b=2
∴直线AB的解析式为:y=-
x+2
;
∵点D(-1,a)在直线AB上,
∴a=
+2
=3
,即D点坐标为(-1,3
),
又∵D点(-1,3
)在反比例函数y=
的图象上,
∴m=-1×3
=-3
,
∴反比例函数的解析式为:y=-
;
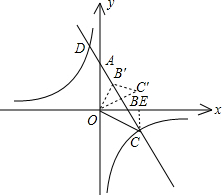
(2)过C点作CE⊥x轴于E,如图,
根据题意得
,解得
或
,
∴C点坐标为(3,-
),
∴OE=3,CE=
,
∴OC=
=2
,
而OA=2
,
∴OA=OC,
又∵OB=2,
∴AB=
=4,
∴∠OAB=30°,
∴∠ACO=30°;
(3)∵∠ACO=30°,
而要OC′⊥AB,
∴∠COC′=90°-30°=60°,
即△OBC绕点O逆时针方向旋转α角(α为锐角),得到△OB′C′,当α为60°时,OC′⊥AB;如图,
∴∠BOB′=60°,
∴点B'在AB上,
而∠OBA=60°,
∴BB′=2,
∴AB′=4-2=2.
把A(0,2
| 3 |
|
| 3 |
| 3 |
∴直线AB的解析式为:y=-
| 3 |
| 3 |
∵点D(-1,a)在直线AB上,
∴a=
| 3 |
| 3 |
| 3 |
| 3 |
又∵D点(-1,3
| 3 |
| m |
| x |
∴m=-1×3
| 3 |
| 3 |
∴反比例函数的解析式为:y=-
3
| ||
| x |
(2)过C点作CE⊥x轴于E,如图,
根据题意得
|
|
|
∴C点坐标为(3,-
| 3 |
∴OE=3,CE=
| 3 |
∴OC=
32+(
|
| 3 |
而OA=2
| 3 |
∴OA=OC,
又∵OB=2,
∴AB=
(2
|
∴∠OAB=30°,
∴∠ACO=30°;
(3)∵∠ACO=30°,
而要OC′⊥AB,
∴∠COC′=90°-30°=60°,
即△OBC绕点O逆时针方向旋转α角(α为锐角),得到△OB′C′,当α为60°时,OC′⊥AB;如图,
∴∠BOB′=60°,
∴点B'在AB上,
而∠OBA=60°,
∴BB′=2,
∴AB′=4-2=2.


练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目