题目内容
【题目】如图，平行四边形ABCD的对角线AC与BD相交于点O，按以下步骤作图：①以点A为圆心，以任意长为半径作弧，分别交AO，AB于点M，N；②以点O为圆心，以AM长为半径作弧，交OC于点M'；③以点M'为圆心，以MN长为半径作弧，在∠COB内部交前面的弧于点N'；④过点N'作射线ON'交BC于点E．若AB＝8，则线段OE的长为_______．
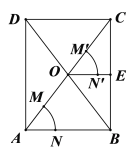
【答案】4
【解析】
利用作法得到∠COE=∠OAB，则OE//AB,利用平行四边形的性质判断OE为△A BC的中位线，从而得到OE的长.
解：由作法得∠COE＝∠OAB，
∴OE∥AB，
∵四边形ABCD为平行四边形，
∴OC＝OA，
∴CE＝BE，
∴OE为△ABC的中位线，
∴OE＝
AB＝×8＝4．
故答案为4．
练习册系列答案
相关题目
