题目内容
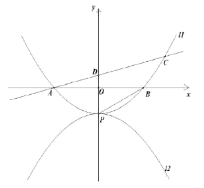
【题目】如图，已知一个抛物线经过A（0，1），B（1，3），C（﹣1，1）三点．
（1）求这个抛物线的表达式及其顶点D的坐标；
（2）联结AB、BC、CA，求tan∠ABC的值；
（3）如果点E在该抛物线的对称轴上，且以点A、B、C、E为顶点的四边形是梯形，直接写出点E的坐标．
【答案】（1）y＝x2+x+1，顶点D的坐标（﹣
，
）；（2）tan∠ABC＝
；（3）点E的坐标为（﹣，3）或（﹣，2）或（﹣，）
【解析】
（1）设抛物线的解析式为y＝ax2+bx+c，将A（0，1）、B（1，3）、C（﹣1，1）代入，求a、b、c的值，可得结果；
（2）如图，过点B作BF⊥x轴于F，延长CA交BF于点D，过点A作AM⊥BC于M，通过勾股定理和等腰直角三角形的性质可求AM和BM的长，即可求解；
（3）分三种情况讨论，由梯形的性质可求解．
解：（1）设抛物线的解析式为y＝ax2+bx+c（a≠0）．
由题意可得：
解得：
∴抛物线的解析式为：y＝x2+x+1，
∵y＝x2+x+1＝
，
∴顶点D的坐标（﹣，）；
（2）如图，过点B作BF⊥x轴于F，延长CA交BF于点D，过点A作AM⊥BC于M，
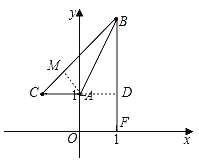
∴BF＝3，
∵A（0，1），C（﹣1，1），
∴AC∥x轴，
∴CD⊥BF，
∴CD＝BD＝2，AD＝1，CA＝1，
∴BC＝2
，∠BCD＝∠CBD＝45°，
∵AM⊥BC，
∴∠MAC＝∠MCA＝45°，
∴CM＝AM，
∴CM＝AM＝
，
∴BM＝BC﹣CM＝
，
∴tan∠ABC＝
＝；
（3）∵A（0，1），B（1，3），C（﹣1，1），
∴直线AC解析式为：y＝1，
直线AB解析式为：y＝2x+1，
直线BC解析式为：y＝x+2，
若BE∥AC，则点E的纵坐标为3，且点E在对称轴上，
∴点E（﹣，3）；
若CE∥AB，则CE的解析式为；y＝2x+3，
∵点E在对称轴上，
∴x＝﹣，
∴y＝2，
即点E（﹣，2）；
若AE∥BC，则AE解析式为：y＝x+1，
∵点E在对称轴上，
∴x＝﹣，
∴y＝，
即点E（﹣，），
综上所述：点E的坐标为（﹣，3）或（﹣，2）或（﹣，）．
