ЬтФПФкШн
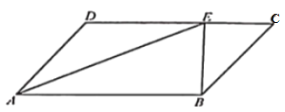
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуOЮЊзјБъдЕуЃЌжБЯпyЃНЉ![]() x+8НЛxжсгкЕуAЃЌНЛyжсгкЕуBЃЌЕуCдкABЩЯЃЌACЃН5ЃЌCDЁЮOAЃЌCDНЛyжсгкЕуDЃЎ
x+8НЛxжсгкЕуAЃЌНЛyжсгкЕуBЃЌЕуCдкABЩЯЃЌACЃН5ЃЌCDЁЮOAЃЌCDНЛyжсгкЕуDЃЎ
ЃЈ1ЃЉЧѓЕуDЕФзјБъЃЛ
ЃЈ2ЃЉЕуPДгЕуOГіЗЂЃЌвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШбиOAдШЫйдЫЖЏЃЌЭЌЪБЕуQДгЕуAГіЗЂЃЌвдУПУы![]() ИіЕЅЮЛГЄЖШЕФЫйЖШбиABдШЫйдЫЖЏЃЌЩшЕуPдЫЖЏЕФЪБМфЮЊtУыЃЈ0ЃМtЃМ3ЃЉЃЌЁїPCQЕФУцЛ§ЮЊSЃЌЧѓSгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ИіЕЅЮЛГЄЖШЕФЫйЖШбиABдШЫйдЫЖЏЃЌЩшЕуPдЫЖЏЕФЪБМфЮЊtУыЃЈ0ЃМtЃМ3ЃЉЃЌЁїPCQЕФУцЛ§ЮЊSЃЌЧѓSгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЙ§ЕуQзїRQЁЭABНЛyжсгкЕуRЃЌСЌНгADЃЌЕуEЮЊADжаЕуЃЌСЌНгOEЃЌЧѓtЮЊКЮжЕЪБЃЌжБЯпPRгыxжсЯрНЛЫљГЩЕФШёНЧгыЁЯOEDЛЅгрЃЎ
ЁОД№АИЁПЃЈ1ЃЉDЃЈ0ЃЌ4ЃЉЃЛЃЈ2ЃЉS=![]() t2Љ6t+12ЃЛЃЈ3ЃЉtЃН
t2Љ6t+12ЃЛЃЈ3ЃЉtЃН![]() Лђ
Лђ![]()
ЁОНтЮіЁП
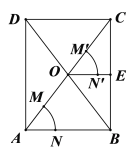
ЃЈ1ЃЉЪзЯШжЄУїAC=BCЃЌРћгУЦНааЯпЕШЗжЯпЖЮЖЈРэЭЦГіOD=BD=4МДПЩНтОіЮЪЬтЃЎ
ЃЈ2ЃЉШчЭМ2ЃЌзїPFЁЭABгкЕуFЃЌЧѓГіPFЃЌCQМДПЩНтОіЮЪЬтЃЎ
ЃЈ3ЃЉЗжСНжжЧщаЮЃКЕБRдкyжсЕФИКАыжсЩЯЃЌШчЭМ3жаЃЌЕБRдкyжсЕФе§АыжсЩЯЃЌШчЭМ4жаЃЌгУСНжжЗНЗЈЧѓГіORЃЌЙЙНЈЗНГЬМДПЩНтОіЮЪЬтЃЎ
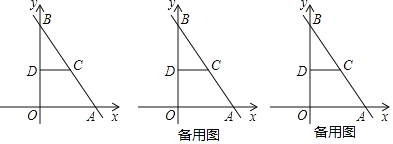
НтЃКЃЈ1ЃЉШчЭМ1жаЃЌ
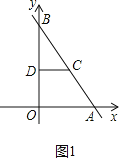
ЁпжБЯпyЃНЉ![]() x+8НЛxжсгкЕуAЃЌНЛyжсгкЕуBЃЌ
x+8НЛxжсгкЕуAЃЌНЛyжсгкЕуBЃЌ
ЁрAЃЈ6ЃЌ0ЃЉЃЌBЃЈ0ЃЌ8ЃЉ
ЁрOAЃН6ЃЌOBЃН8ЃЌ
ЁрABЃН![]() ЃН
ЃН![]() ЃН10ЃЌ
ЃН10ЃЌ
ЁпACЃН5ЃЌ
ЁрACЃНBCЃН5ЃЌ
ЁпCDЁЮOAЃЌ
ЁрBDЃНODЃН4ЃЌ
ЁрDЃЈ0ЃЌ4ЃЉЃЎ
ЃЈ2ЃЉШчЭМ2ЃЌзїPFЁЭABгкЕуFЃЌPAЃН6Љt
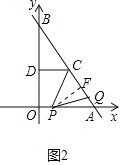
PFЃНPAsinЁЯPAFЃН![]() ЃЈ6ЉtЃЉЃЌ
ЃЈ6ЉtЃЉЃЌ
ЁрCQЃН5Љ![]() tЃЌ
tЃЌ
SЃН![]() CQPFЃН
CQPFЃН![]() ЃЈ5Љ
ЃЈ5Љ![]() tЃЉ
tЃЉ![]() ЃЈ6ЉtЃЉЃН
ЃЈ6ЉtЃЉЃН![]() t2Љ6t+12ЃЎ
t2Љ6t+12ЃЎ
ЃЈ3ЃЉШчЭМ3жаЃЌзїOGЁЭAD гкЕуGЃЌ
дкRtЁїAODжаЃЌADЃН![]() ЃН
ЃН![]() ЃН2
ЃН2![]() ЃЌ
ЃЌ
ЁпSЁїAODЃН![]() ODOAЃН
ODOAЃН![]() ADOG
ADOG
ЁрOGЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрDGЃН![]() ЃН
ЃН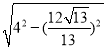 ЃН
ЃН![]() ЃЌ
ЃЌ
ЁпDEЃНAEЃН![]() ЃЌ
ЃЌ
ЁрGEЃНDEЉDGЃН![]() Љ
Љ![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁпЁЯOED+ЁЯOPRЃН90ЁуЃЌЁЯOED+ЁЯEOGЃН90ЁуЃЌ
ЁрЁЯOPRЃНЁЯEOGЃЌ
ЁрtanЁЯOPRЃНtanЁЯEOGЃН![]()
ЁпBRЃН![]() ЃН
ЃН ЃН
ЃН![]() Љ
Љ![]() tЃЌ
tЃЌ
ЁпtanЁЯOPRЃН![]() ЃН
ЃН![]() ЃЌOPЃНtЃЌ
ЃЌOPЃНtЃЌ
ЁрORЃН![]() tЃЌ
tЃЌ
ЕБRдкyжсЕФИКАыжсЩЯЃЌШчЭМ3жаЃЌ

ORЃНBRЉ8ЃН![]() Љ
Љ![]() tЃЌ
tЃЌ
Ёр![]() tЃН
tЃН![]() Љ
Љ![]() tЃЌ
tЃЌ
НтЕУtЃН![]() ЃЌ
ЃЌ
ЕБRдкyжсЕФе§АыжсЩЯЃЌШчЭМ4жаЃЌ
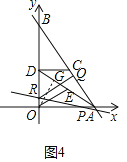
ORЃН8ЉBRЃН![]() tЉ
tЉ![]() ЃЌ
ЃЌ
Ёр![]() tЃН
tЃН![]() tЉ
tЉ![]() ЃЌ
ЃЌ
НтЕУtЃН![]() ЃЌ
ЃЌ
злЩЯЃЌЕБtжЕЮЊ![]() Лђ
Лђ![]() ЃЌжБЯпPRгыxжсЯрНЛЫљГЩЕФШёНЧгыЁЯOEDЛЅгрЃЎ
ЃЌжБЯпPRгыxжсЯрНЛЫљГЩЕФШёНЧгыЁЯOEDЛЅгрЃЎ