Question

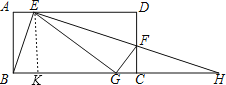
【题目】如图，将矩形ABCD的一个角翻折，使得点D恰好落在BC边上的点G处，折痕为EF，若EB为∠AEG的平分线，EF和BC的延长线交于点H．下列结论中：①∠BEF＝90°；②DE＝CH；③BE＝EF；④△BEG和△HEG的面积相等；⑤若，则．以上命题，正确的有（　　）

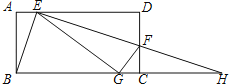
A.2个B.3个C.4个D.5个

Answer 1

【答案】B

【解析】

①根据平角的定义，折叠的性质和角平分线的性质即可作出判断；

②根据折叠的性质和等腰三角形的性质可知DE≠CH；

③无法证明BE＝EF；

④根据角平分线的性质，等腰三角形的性质和三角形中线的性质可得△BEG和△HEG的面积相等；

⑤过E点作EK⊥BC，垂足为K，在RT△EKG中利用勾股定理可做出判断.

解：①由折叠的性质可知∠DEF＝∠GEF，∵EB为∠AEG的平分线，∴∠AEB＝∠GEB，∵∠AED＝180°，∴∠BEF＝90°，故正确；

②根据矩形的性质可得∠D=∠FCH,∠DFE=∠CFH（对顶角相等）

所以△EDF∽△HCF，DF＞CF，故DE≠CH，故错误；

③无法证明BE＝EF，故错误；

④∵ABCD是矩形，

∴∠AEB=∠EBC（内错角相等）

又∵EB为∠AEG的平分线，

∴∠AEB=∠BEG,

∴∠BEG=∠EBC，

∴△GEB是等腰三角形，

∵ABCD是矩形，

∴∠DEF=∠CHF（内错角相等），

又∵折叠的性质得到∠DEF=∠FEG,

∴∠FEG=∠CHF，

∴△GEH是等腰三角形，

则G是BH边的中线，

∴△BEG和△HEG的面积相等，故正确；

⑤过E点作EK⊥BC，垂足为K.设BK=x，CD=y，由可得AD=2y

∵EB平分∠AEG，

∴∠AEB=∠BEG，

又∵AD∥BC，

∴∠AEB=∠EBG，

∴∠BEG=∠EBG，

∴BG=EG

在RT△EKG中，，，

，由勾股定理有，即，解得，当时，，K、G重合，不符合题意，舍去。故取，此时，则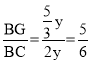，故正确的有3个．

故选:B．