Question

【题目】模具厂计划生产面积为4，周长为m的矩形模具．对于m的取值范围，小亮已经能用“代数”的方法解决，现在他又尝试从“图形”的角度进行探究，过程如下：

（1）建立函数模型

设矩形相邻两边的长分别为x，y，由矩形的面积为4，得，即；由周长为m，得，即．满足要求的应是两个函数图象在第　 　象限内交点的坐标．

（2）画出函数图象

函数的图象如图所示，而函数的图象可由直线平移得到．请在同一直角坐标系中直接画出直线．

（3）平移直线，观察函数图象

①当直线平移到与函数的图象有唯一交点时，周长m的值为　 　；

②在直线平移过程中，交点个数还有哪些情况？请写出交点个数及对应的周长m的取值范围．

（4）得出结论

若能生产出面积为4的矩形模具，则周长m的取值范围为　 　．

Answer 1

【答案】（1）一（2）见解析（3）①②；（4）

【解析】

（1）x，y都是边长，因此，都是正数，即可求解；

（2）直接画出图象即可；

（3）①把点代入即可求解；②在直线平移过程中，交点个数有：0个、1个、2个三种情况，联立和并整理得：，即可求解；

（4）运用（3）的相关结论即可．

解：（1）x，y都是边长，因此，都是正数，

故点在第一象限，

答案为：一；

（2）图象如下所示：

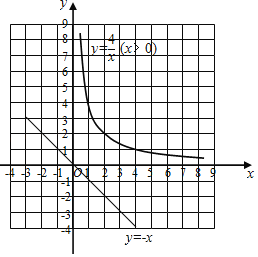
（3）①把点代入得：

，解得：；

②在直线平移过程中，交点个数有：0个、1个、2个三种情况，

联立和并整理得：，

时，两个函数有交点，

解得：；

（4）由（3）得：．