题目内容
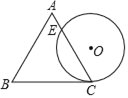
【题目】如图，点
为线段
上一点，分别以
为底作顶角为
的等腰三角形，顶角顶点分别为
(点
在的同侧，点
在的另一侧)
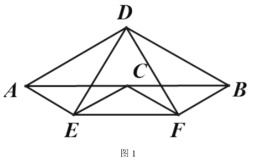
（1）如图 1，若点是的中点，则
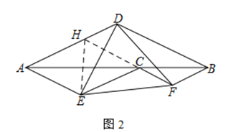
（2）如图 2，若点不是的中点，①求证：
为等边三角形；
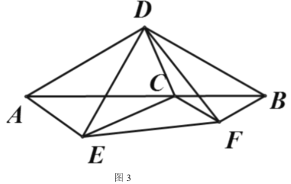
②如图 3，连接
，若
，求
的长．
【答案】（1）30；（2）①见解析；②
【解析】
（1）过
作
于
，连接
，先求出∠EAC=∠ACE=30°，设
，得到
，再求出DC=CE=2x，根据等腰三角形的性质及平行线的性质得到
，得到
，再根据三角形内角和求出答案；
（2）①延长
交
于，连接
，先证明
，
，得到四边形
、四边形
是平行四边形，证得△AEH是等边三角形，再证明
≌△FCE得到DE=EF，∠DEF=∠CEH=60°，由此得到结论；
②过作
于
，利用已知及直角三角形30°角所对直角边等于斜边一半的性质求出AC=2，
，根据等腰三角形的性质求出CM=1，根据
求出CE，再根据勾股定理求出DE，即可得到EF.
解：（1）如图1，过作于，连接，
∵AE=CE，∠AEC=120°，
∴∠EAC=∠ACE=30°，
设，则
，
，
，
，
是
的中点，
，
，
，
，
，
，
，
，
，
，
，
，
∵∠DAE=∠DAC+∠EAC=60°，
∴∠ADE=180°-∠DAE-∠AED=30°，
故答案为：30；
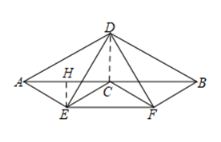
（2）①延长交于，连接，如图2，
，
，
，
，
同理：
，
，
，
，
同理，
四边形、四边形是平行四边形，
，
，
，
，
，
是等边三角形，
，
，
，
．
，
∴≌△FCE(SAS)，
，
，
，
是等边三角形；
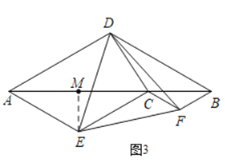
②如图3，过作于，
，
，
，
，
，
，
，
∴AC=2，，
，
，
，
，
，
，
，
中，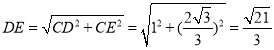
，
由①知：
是等边三角形，
．
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
