题目内容
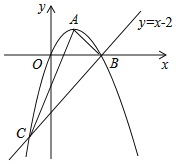
【题目】如图,已知抛物线经过原点O,顶点为A(1,1),且与直线![]() 交于B,C两点.
交于B,C两点.
(1)求抛物线的解析式及点C的坐标;
(2)求△ABC的面积;
(3)若点N为x轴上的一个动点,过点N作MN⊥x轴与抛物线交于点M,则是否存在以O,M,N为顶点的三角形与△ABC相似?若存在,请求出点N的坐标;若不存在,请说明理由.
【答案】(1)y=﹣(x﹣1)2+1,C(﹣1,﹣3);(2)3;(3)存在满足条件的N点,其坐标为(![]() ,0)或(
,0)或(![]() ,0)或(﹣1,0)或(5,0)
,0)或(﹣1,0)或(5,0)
【解析】
(1)可设顶点式,把原点坐标代入可求得抛物线解析式,联立直线与抛物线解析式,可求得C点坐标;
(2)设直线AC的解析式为y=kx+b,与x轴交于D,得到y=2x1,求得BD于是得到结论;
(3)设出N点坐标,可表示出M点坐标,从而可表示出MN、ON的长度,当△MON和△ABC相似时,利用三角形相似的性质可得![]() 或
或![]() ,可求得N点的坐标.
,可求得N点的坐标.
(1)∵顶点坐标为(1,1),
∴设抛物线解析式为y=a(x﹣1)2+1,又抛物线过原点,
∴0=a(0﹣1)2+1,解得a=﹣1,∴抛物线解析式为y=﹣(x﹣1)2+1,
即y=﹣x2+2x,联立抛物线和直线解析式可得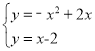 ,
,
解得![]() 或
或![]() ,∴B(2,0),C(﹣1,﹣3);
,∴B(2,0),C(﹣1,﹣3);
(2)设直线AC的解析式为y=kx+b,与x轴交于D,
把A(1,1),C(﹣1,﹣3)的坐标代入得![]() ,
,
解得:![]() ,
,
∴y=2x﹣1,当y=0,即2x﹣1=0,解得:x=![]() ,∴D(
,∴D(![]() ,0),
,0),
∴BD=2﹣![]() =
=![]() ,
,
∴△ABC的面积=S△ABD+S△BCD=![]() ×
×![]() ×1+
×1+![]() ×
×![]() ×3=3;
×3=3;
(3)假设存在满足条件的点N,设N(x,0),则(x,﹣x2+2x),
∴ON=|x|,MN=|﹣x2+2x|,由(2)知,AB=![]() ,BC=3
,BC=3![]() ,
,
∵MN⊥x轴于点N,∴∠ABC=∠MNO=90°,
∴当△ABC和△MNO相似时,有![]() 或
或![]() ,
,
①当![]() 时,∴
时,∴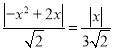 ,即|x||﹣x+2|=
,即|x||﹣x+2|=![]() |x|,
|x|,
∵当x=0时M、O、N不能构成三角形,∴x≠0,∴|﹣x+2|=![]() ,∴﹣x+2=±
,∴﹣x+2=±![]() ,解得x=
,解得x=![]() 或x=
或x=![]() ,此时N点坐标为(
,此时N点坐标为(![]() ,0)或(
,0)或(![]() ,0);
,0);
②当或![]() 时,∴
时,∴ ,即|x||﹣x+2|=3|x|,
,即|x||﹣x+2|=3|x|,
∴|﹣x+2|=3,∴﹣x+2=±3,解得x=5或x=﹣1,
此时N点坐标为(﹣1,0)或(5,0),
综上可知存在满足条件的N点,其坐标为(![]() ,0)或(
,0)或(![]() ,0)或(﹣1,0)或(5,0).
,0)或(﹣1,0)或(5,0).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
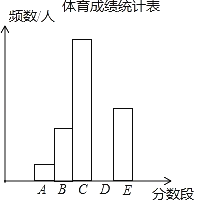
小学生10分钟应用题系列答案【题目】为了了解某市九年级学生的体育成绩(成绩均为整数),随机抽取了部分学生的体育成绩并分段(A:20.5~22.5;B:22.5~24.5;C:24.5~26.5;D:26.5~28.5;E:28.5~30.5)统计,得到统计图、表如图.
分数段 | A | B | C | D | E | 合计 |
频数/人 | 12 | 36 | 84 | b | 48 | c |
频率 | 0.05 | a | 0.35 | 0.25 | 0.20 | 1 |
根据上面的信息,回答下列问题:
(1)统计表中,a= ,b= ,c= ;将频数分布直方图补充完整.
(2)小明说:“这组数据的众数一定在C中.”你认为小明的说法正确吗? (选填“正确”或“错误”).
(3)若成绩在27分及以上定为优秀,则该市30000名九年级学生中体育成绩为优秀的学生人数约有多少?