Question

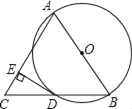
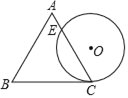
【题目】如图是某商品标牌的示意图，⊙O与等边△ABC的边BC相切于点C，且⊙O的直径与△ABC的高相等，已知等边△ABC边长为4，设⊙O与AC相交于点E，则AE的长为（　　）

A.B.1C.﹣1D.

Answer 1

【答案】B

【解析】

通过求解CE的长度来求出AE的长，连接OC，并过点O作OF⊥CE于F，求出等边三角形的高即可得出⊙O的直径，进而得到半径OC的长度；根据切线和等边三角形的性质不难的得出∠OCF=30°，再在Rt△OFC中，利用特殊角的三角函数值求出FC的长，最后利用垂径定理即可得出CE的长.

连接OC，并过点O作OF⊥CE于F.

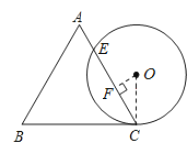
∵△ABC为等边三角形，边长为4，

∴∠ACB=60°，△ABC的高为2.

∵等边三角形ABC的高与⊙O的直径相等，

∴⊙O的半径OC=.

∵⊙O与BC相切于点C，

∴∠OCB=90°.

∵∠ACB=60°，

∴∠OCF=30°.

∵在Rt△OFC中，∠OCF=30°，OC=，

∴FC=，

∴CE=2FC=3（cm）

∴AE=AC-CE=4-3=1（cm）

故选B.