题目内容
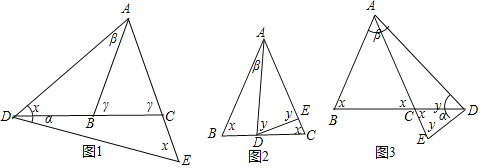
【题目】如图,△ABC中,∠ABC=∠ACB,点D在BC所在的直线上,点E在射线AC上,且AD=AE,连接DE.
⑴如图①,若∠B=∠C=35°,∠BAD=80°,求∠CDE的度数;
⑵如图②,若∠ABC=∠ACB=75°,∠CDE=18°,求∠BAD的度数;
⑶当点D在直线BC上(不与点B、C重合)运动时,试探究∠BAD与∠CDE的数量关系,并说明理由.

【答案】(1)40°;(2)36°;(3)∠BAD与∠CDE的数量关系是2∠CDE=∠BAD.
【解析】试题分析:(1)根据等腰三角形的性质得到∠BAC=110°,根据等腰三角形的性质和三角形的外角的性质即可得到结论; (2)根据三角形的外角的性质得到∠E=75°-18°=57°,根据等腰三角形的性质和三角形的外角的性质即可得到结论; (3)设∠ABC=∠ACB=y°,∠ADE=∠AED=x°,∠CDE=α,∠BAD=β,分3种情况:①如图1,当点D在点B的左侧时,∠ADC=x°-α,②如图2,当点D在线段BC上时,∠ADC=y°+α,③如图3,当点D在点C右侧时,∠ADC=y°-α,根据这3种情况分别列方程组即,解方程组即可得到结论.
试题解析:
(1)∵∠B=∠C=35°,
∴∠BAC=110° ,
∵∠BAD=80°,
∴∠DAE=30°,
∵AD=AE,
∴∠ADE=∠AED=75°,
∴∠CDE=∠AED-∠C=75°35°=40°;
(2)∵∠ACB=75°,∠CDE=18° ,
∴∠E=75°18°=57°,
∴∠ADE=∠AED=57°,
∴∠ADC=39°,
∵∠ABC=∠ADB+∠DAB=75° ,
∴∠BAD=36°.
(3)设∠ABC=∠ACB=y°,∠ADE=∠AED=x°,∠CDE=α,∠BAD=β
①如图1,当点D在点B的左侧时,∠ADC=x°﹣α
∴![]() ,(1)﹣(2)得,2α﹣β=0,
,(1)﹣(2)得,2α﹣β=0,
∴2α=β;
②如图2,当点D在线段BC上时,∠ADC=y°+α
∴![]() ,(2)﹣(1)得,α=β﹣α,
,(2)﹣(1)得,α=β﹣α,
∴2α=β;
③如图3,当点D在点C右侧时,∠ADC=y°﹣α
∴![]() ,(2)﹣(1)得,2α﹣β=0,
,(2)﹣(1)得,2α﹣β=0,
∴2α=β.
综上所述,∠BAD与∠CDE的数量关系是2∠CDE=∠BAD.

 天天练口算系列答案
天天练口算系列答案【题目】作三角形用到的基本作图是:
(1)___________________________;(2)_______________________________;
【答案】 作一个角等于已知角 作一条线段等于已知线段
【解析】试题解析:作三角形用到的基本作图是:(1). 作一个角等于已知角(2). 作一条线段等于已知线段
故答案为:(1). 作一个角等于已知角(2). 作一条线段等于已知线段.
【题型】填空题
【结束】
10
【题目】尺规作三角形的类型:
尺 规 作 图 | 类型 | 依据 |
已知两边及其夹角作三角形 | __________ | |
已知两角一边作三角形 | __________(或 | |
已知三边作三角形 | __________ |
【题目】某汽车生产厂对其生产的A型汽车进行油耗试验,试验中汽车为匀速行驶,在行驶过程中,油箱的余油量y(升)与行驶时间t(小时)之间的关系如表:
t(小时) | 0 | 1 | 2 | 3 |
y(升) | 120 | 112 | 104 | 96 |
由表格中y与t的关系可知,当汽车行驶_____小时,油箱的余油量为0.



