题目内容
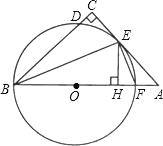
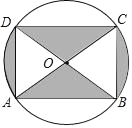
【题目】如图是某商品的标志图案,AC与BD是⊙O的两条直径,首尾顺次连接点A、B、C、D,得到四边形ABCD,若AC=10cm,∠BAC=36°,则图中阴影部分的面积为_____.
【答案】10πcm2.
【解析】分析:根据已知条件得到四边形ABCD是矩形,求得图中阴影部分的面积=S扇形AOD+S扇形BOC=2S扇形AOD,根据等腰三角形的性质得到∠BAC=∠ABO=36°,由圆周角定理得到∠AOD=72°,于是得到结论.
详解:∵AC与BD是⊙O的两条直径,
∴∠ABC=∠ADC=∠DAB=∠BCD=90°,
∴四边形ABCD是矩形,
∴S△ABO=S△CDO =S△AOD=S△BOD,
∴图中阴影部分的面积=S扇形AOD+S扇形BOC=2S扇形AOD,
∵OA=OB,
∴∠BAC=∠ABO=36°,
∴∠AOD=72°,
∴图中阴影部分的面积=2×![]() =10π,
=10π,
故答案为:10πcm2.

练习册系列答案
相关题目
【题目】某检修小组从A地出发,在东西方向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下.(单位:km)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
-4 | +8 | -9 | +8 | +6 | -5 | -2 |
(1)求收工时距A地多远?
(2)若每km耗油0.4升,问一天共耗油多少升?