题目内容
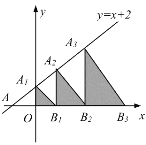
【题目】如图,在平面直角坐标系中,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
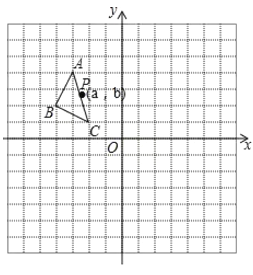
轴于点![]() ,若图中阴影部分的三角形都是等腰直角三角形,则从左往右数第5个阴影三角形的面积是_____,第2019个阴影三角形的面积是_____.
,若图中阴影部分的三角形都是等腰直角三角形,则从左往右数第5个阴影三角形的面积是_____,第2019个阴影三角形的面积是_____.
【答案】![]()
![]()
【解析】
根据一次函数图象上点的坐标特征结合等腰直角三角形的性质,即可得出OA1、A2B1、A3B2、A4B3的值,根据边的长度的变化即可找出变化规律“An+1Bn=BnBn+1=2n+1”,再根据三角形的面积即可得出Sn+1=![]() ×(2n+1)2=22n+1,分别代入n=4、2018即可求出结论.
×(2n+1)2=22n+1,分别代入n=4、2018即可求出结论.
解:当x=0时,y=x+2=2,
∴OA1=OB1=2;
当x=2时,y=x+2=4,
∴A2B1=B1B2=4;
当x=2+4=6时,y=x+2=8,
∴A3B2=B2B3=8;
当x=6+8=14时,y=x+2=16,
∴A4B3=B3B4=16.
∴An+1Bn=BnBn+1=2n+1,
∴Sn+1=![]() ×(2n+1)2=22n+1.
×(2n+1)2=22n+1.
当n=4时,S5=22×4+1=29;当n=2018时,S2019=22×2018+1=24037.
故答案为:29;24037.

练习册系列答案
相关题目