题目内容
【题目】实践操作
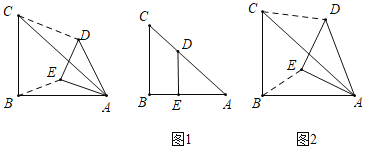
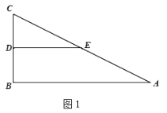
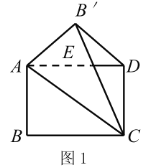
如图1,将矩形纸片![]() 沿对角线
沿对角线![]() 翻折,使点
翻折,使点![]() 落在矩形
落在矩形![]() 所在平面内,
所在平面内,![]() 和
和![]() 相交于点
相交于点![]() ,连接
,连接![]() .
.
解决问题
(1)在图1中,①![]() 和
和![]() 的位置关系为__________;②将
的位置关系为__________;②将![]() 剪下后展开,得到的图形是_____;
剪下后展开,得到的图形是_____;
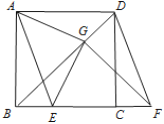
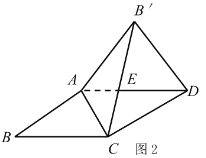
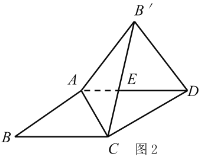
(2)若图1中的矩形变为平行四边形时![]() ,如图2所示,结论①和结论②是否成立,若成立,请挑选其中的一个结论加以证明,若不成立,请说明理由;
,如图2所示,结论①和结论②是否成立,若成立,请挑选其中的一个结论加以证明,若不成立,请说明理由;
拓展应用
(3)小红沿对角线折叠一张矩形纸片,发现所得图形是轴对称图形,沿对称轴再次折叠后,得到的仍是轴对称图形,则小红折叠的矩形纸片的长宽之比为_________.
【答案】(1)①![]() ;②菱形;(2)成立,证明见解析;(3)
;②菱形;(2)成立,证明见解析;(3)![]() 或
或![]()
【解析】
(1)①利用AAS定理求证△![]() ≌△CDE,从而得到DE=
≌△CDE,从而得到DE=![]() ,CE=AE,然后根据等腰三角形的性质求得
,CE=AE,然后根据等腰三角形的性质求得![]() ,然后根据内错角相等两直线平行即可判断;
,然后根据内错角相等两直线平行即可判断;
②根据菱形的判定方法即可解决问题;
(2)只要证明AE=EC,即可证明结论②成立;只要证明∠ADB′=∠DAC,即可推出B′D∥AC;
(3)①当AB:AD=1:1时,符合题意.②当AD:AB=![]() 时,也符合题意
时,也符合题意
解:(1)①由折叠性质可知:![]() ,
,![]()
又∵![]()
∴△![]() ≌△CDE
≌△CDE
∴DE=![]() ,CE=AE,
,CE=AE,
∴![]()
![]() ,
,![]()
又∵![]()
∴![]()
∴![]() ;
;
②由①可知AE=CE,又由折叠性质可知
将![]() 剪下后展开,得到的图形是四条边都相等的四边形,
剪下后展开,得到的图形是四条边都相等的四边形,
又∵∠AEC为钝角
∴将![]() 剪下后展开,得到的图形是菱形;
剪下后展开,得到的图形是菱形;
故答案为:![]() ;菱形;
;菱形;

(2)若选择①证明如下,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() ,
,
![]() 将
将![]() 沿
沿![]() 翻折至
翻折至![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]()
![]() ,
,
![]()
若选择②证明如下:
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() ,
,
![]() ,
,
![]() 将
将![]() 沿
沿![]() 翻折至
翻折至![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是等腰三角形;
是等腰三角形;
![]() 将
将![]() 剪下后展开,得到的图形四边相等,
剪下后展开,得到的图形四边相等,
![]() 将
将![]() 剪下后展开,得到的图形是菱形.
剪下后展开,得到的图形是菱形.
(3)如图中,
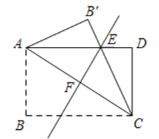
①当AB:AD=1:1时,四边形ABCD是正方形,
∴∠BAC=∠CAD=∠EAB′=45°,
∵AE=AE,∠B′=∠AFE=90°,
∴△AEB′≌△AEF(AAS),
∴AB′=AF,
此时四边形AFEB′是轴对称图形,符合题意.
②当AD:AB=![]() 时,也符合题意,
时,也符合题意,
∵此时∠DAC=30°,
∴AC=2CD,
∴AF=FC=CD=AB=AB′,
∴此时四边形AFEB′是轴对称图形,符合题意.
综上所述,满足条件的矩形纸片的长宽之比为![]() 或
或![]() .
.