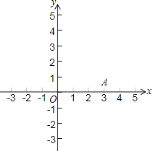题目内容
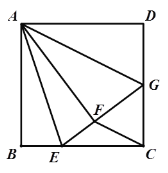
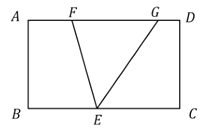
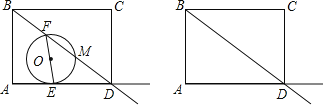
【题目】如图,矩形ABCD中,AB=6,AD=8.动点E,F同时分别从点A,B出发,分别沿着射线AD和射线BD的方向均以每秒1个单位的速度运动,连接EF,以EF为直径作⊙O交射线BD于点M,设运动的时间为t.
(1)当点E在线段AD上时,用关于t的代数式表示DE,DM.
(2)在整个运动过程中,
①连结CM,当t为何值时,△CDM为等腰三角形.
②圆心O处在矩形ABCD内(包括边界)时,求t的取值范围,并直接写出在此范围内圆心运动的路径长.
【答案】(1)(1)ED=8﹣t,MD=![]() .(2)①t=
.(2)①t=![]() 或t=
或t=![]() 或t=
或t=![]() ;②0≤t≤
;②0≤t≤![]() ,圆心运动的路径长为
,圆心运动的路径长为![]()
【解析】
(1)在Rt△ABD中,依据勾股定理可求得BD的长,然后依据MD=EDcos∠MDE,cos∠MDE=cos∠ADB=![]() ,由此即可解决问题.
,由此即可解决问题.
(2)①可分为点E在AD上,点E在AD的延长线上画出图形,然后再依据MC=MD,CM=CD、DM=DC三种情况求解即可;
②当t=0时,圆心O在AB边上.当圆心O在CD边上时,过点E作EH∥CD交BD的延长线与点H.先求得DH的长,然后依据平行线分线段成比例定理可得到DF=DH,然后依据DF=DH列出关于t的方程,从而可求得t的值,故此可得到t的取值范围.
解:(1)如图1所示:连接ME.
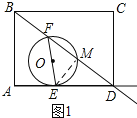
∵AE=t,AD=8,
∴ED=AD-AE=8-t.
∵EF为⊙O的直径,
∴∠EMF=90°.
∴∠EMD=90°.
∴MD=EDcos∠MDE=![]() .
.
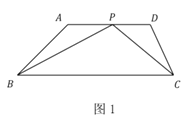
(2)①a、如图2所示:连接MC.
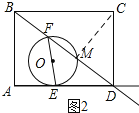
当DM=CD=6时,![]() =6,解得t=
=6,解得t=![]() ;
;
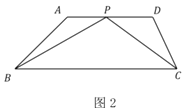
b、如图3所示:当MC=MD时,连接MC,过点M作MN⊥CD,垂足为N.
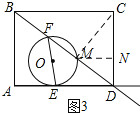
∵MC=MD,MN⊥CD,
∴DN=NC.
∵MN⊥CD,BC⊥CD,
∴BC∥MN.
∴M为BD的中点.
∴MD=5,即![]() =5,解得t=
=5,解得t=![]() ;
;
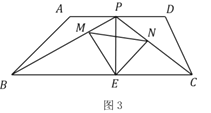
c、如图4所示:CM=CD时,过点C作CG⊥DM.
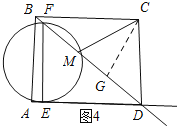
∵CM=CD,CG⊥MD,
∴GD=![]() MD=
MD=![]() .
.
∵![]() ,
,
∴DG=![]() CD=
CD=![]() .
.
∴![]() =
=![]() .
.
解得:t=-1(舍去).
d、如图5所示:当CD=DM时,连接EM.

∵AE=t,AD=8,
∴DE=t-8.
∵EF为⊙O的直径,
∴EM⊥DM.
∴DM=EDcos∠EDM=![]() .
.
∴![]() =6,解得:t=
=6,解得:t=![]() .
.
综上所述,当t=![]() 或t=
或t=![]() 或t=
或t=![]() 时,△DCM为等腰三角形.
时,△DCM为等腰三角形.
②当t=0时,圆心O在AB边上.
如图6所示:当圆心O在CD边上时,过点E作EH∥CD交BD的延长线与点H.

∵HE∥CD,OF=OE,
∴DF=DH.
∵DH=![]() =
=![]() ,DF=10-t,
,DF=10-t,
∴![]() =10-t.
=10-t.
解得:t=![]() .
.
综上所述,在整个运动过程中圆心O处在矩形ABCD内(包括边界)时,t的取值范围为0≤t≤![]() .
.
此时点O的运动路径为OO1的长度,如图:
过点O作OM⊥AB
当t=![]() 时,DE=
时,DE=![]() -8=
-8=![]()
∵EH∥CD,AB∥CD
∴EH∥AB
∴△DEH∽△DAB
∴![]() ,即
,即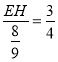 ,解得EH=
,解得EH=![]()
∴OD=![]() EH=
EH=![]()
由题意可知四边形ADOK是矩形
∴AK= OD =![]() ,OK=AD=8
,OK=AD=8
∴O1K= O1A- AK=![]()
在Rt△OKO1中,OO1=![]()
∴圆心运动的路径长为![]() .
.

【题目】参照学习函数的过程与方法,探究函数![]() 的图象与性质.因为
的图象与性质.因为![]() ,即
,即![]() ,所以我们对比函数
,所以我们对比函数![]() 来探究.
来探究.
列表:
| … | -4 | -3 | -2 | -1 |
|
|
| 2 | 3 | 4 | … |
| … |
|
| 1 | 2 | 4 | -4 | -1 |
| … | ||
| … |
|
| 2 | 3 | 5 | -3 | -1 | 0 |
|
| … |
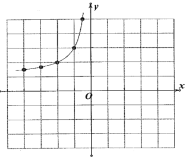
描点:在平面直角坐标系中,以自变量![]() 的取值为横坐标,以
的取值为横坐标,以![]() 相应的函数值为纵坐标,描出相应的点,如图所示:
相应的函数值为纵坐标,描出相应的点,如图所示:
(1)①请补全表格,计算![]() __________.
__________.
②请补全图形,用一条光滑曲线顺次连接起来;
(2)观察图象并分析表格,回答下列问题:
①当![]() 时,
时,![]() 随
随![]() 的增大而__________;(填“增大”或“减小”)
的增大而__________;(填“增大”或“减小”)
②![]() 的图象是由
的图象是由![]() 的图象向__________平移__________
的图象向__________平移__________
③图象关于点__________中心对称.(填点的坐标)
(3)结合函数图象,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.