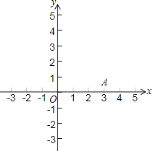题目内容
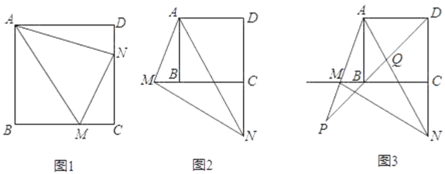
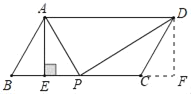
【题目】如图,在ABCD中,已知AD=10cm,tanB=2,AE⊥BC于点E,且AE=4cm,点P是BC边上一动点.若△PAD为直角三角形,则BP的长为_____

【答案】2cm或4cm或10cm
【解析】
由三角函数得出BE=2,分两种情况:
①当∠PAD=90°时,点P与E重合,BP=BE=2;
②当∠APD=90°时,作DF⊥ABC于F,则∠DFP=∠AEP=90°,DF=AE=4,证明△APE∽△PDF,得出![]() ,解得PE=2,或PE=8,得出BP=BE+PE=4,或BP=BE+PE=10;即可得出答案.
,解得PE=2,或PE=8,得出BP=BE+PE=4,或BP=BE+PE=10;即可得出答案.
解:∵AE⊥BC,
∴∠AEB=∠AEC=90°,
∵tanB=![]() =2,且AE=4,
=2,且AE=4,
∴BE=2,
分两种情况:
①当∠PAD=90°时,点P与E重合,BP=BE=2;
②当∠APD=90°时,作DF⊥ABC于F,如图所示:
则∠DFP=∠AEP=90°,DF=AE=4,
∵∠APE+∠PAE=∠APE+∠DPF=90°,
∴∠PAE=∠DPF,
∴△APE∽△PDF,
∴![]() ,即
,即![]() =
=![]() ,
,
解得:PE=2,或PE=8,
∴BP═BE+PE=4,或BP=BE+PE=10
综上所述,若△PAD为直角三角形,则BP的长为2cm或4cm或10cm;
故答案为:2cm或4cm或10cm.

【题目】为了解某区八年级学生的睡眠情况,随机抽取了该区八年级学生部分学生进行调查.已知D组的学生有15人,利用抽样所得的数据绘制所示的统计图表.
一、学生睡眠情况分组表(单位:小时)
组别 | 睡眠时间 |
|
|
|
|
|
|
|
|
|
|
二、学生睡眠情况统计图
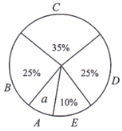
根据图表提供的信息,回答下列问题:
(1)试求“八年级学生睡眠情况统计图”中的a的值及a对应的扇形的圆心角度数;
(2)如果睡眠时间x(时)满足:![]() ,称睡眠时间合格.已知该区八年级学生有3250人,试估计该区八年级学生睡眠时间合格的共有多少人?
,称睡眠时间合格.已知该区八年级学生有3250人,试估计该区八年级学生睡眠时间合格的共有多少人?
(3)如果将各组别学生睡眠情况分组的最小值(如C组别中,取![]() ),B、C、D三组学生的平均睡眠时间作为八年级学生的睡眠时间的依据.试求该区八年级学生的平均睡眠时间.
),B、C、D三组学生的平均睡眠时间作为八年级学生的睡眠时间的依据.试求该区八年级学生的平均睡眠时间.
【题目】参照学习函数的过程与方法,探究函数![]() 的图象与性质.因为
的图象与性质.因为![]() ,即
,即![]() ,所以我们对比函数
,所以我们对比函数![]() 来探究.
来探究.
列表:
| … | -4 | -3 | -2 | -1 |
|
|
| 2 | 3 | 4 | … |
| … |
|
| 1 | 2 | 4 | -4 | -1 |
| … | ||
| … |
|
| 2 | 3 | 5 | -3 | -1 | 0 |
|
| … |
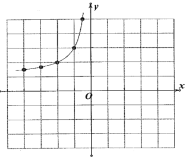
描点:在平面直角坐标系中,以自变量![]() 的取值为横坐标,以
的取值为横坐标,以![]() 相应的函数值为纵坐标,描出相应的点,如图所示:
相应的函数值为纵坐标,描出相应的点,如图所示:
(1)①请补全表格,计算![]() __________.
__________.
②请补全图形,用一条光滑曲线顺次连接起来;
(2)观察图象并分析表格,回答下列问题:
①当![]() 时,
时,![]() 随
随![]() 的增大而__________;(填“增大”或“减小”)
的增大而__________;(填“增大”或“减小”)
②![]() 的图象是由
的图象是由![]() 的图象向__________平移__________
的图象向__________平移__________
③图象关于点__________中心对称.(填点的坐标)
(3)结合函数图象,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.