题目内容
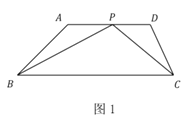
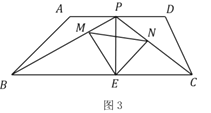
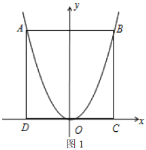
【题目】如图1,在矩形纸片![]() 中,
中,![]() ,
,![]() ,折叠纸片使
,折叠纸片使![]() 点落在边
点落在边![]() 上的
上的![]() 处,折痕为
处,折痕为![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.

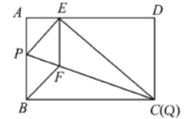
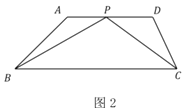
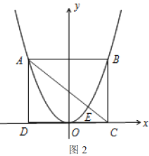
图1 图2
(1)求证:四边形![]() 为菱形;
为菱形;
(2)当点![]() 在
在![]() 边上移动时,折痕的端点
边上移动时,折痕的端点![]() ,
,![]() 也随之移动;
也随之移动;
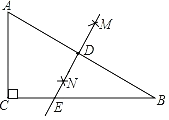
①当点![]() 与点
与点![]() 重合时(如图2),求菱形
重合时(如图2),求菱形![]() 的边长;
的边长;
②若限定![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上移动,则点
上移动,则点![]() 在边
在边![]() 上移动的最大距离是_______.
上移动的最大距离是_______.
【答案】(1)见解析;(2)①![]() ;②点
;②点![]() 在边
在边![]() 上移动的最大距离为
上移动的最大距离为![]()
【解析】
(1)由折叠的性质得出![]() ,
,![]() ,
,![]() ,由平行线的性质得出
,由平行线的性质得出![]() ,证出
,证出![]() ,得出
,得出![]() ,因此
,因此![]() ,即可得出结论;
,即可得出结论;
(2)①由矩形的性质得出![]() ,
,![]() ,
,![]() ,由对称的性质得出
,由对称的性质得出![]() ,在
,在![]() 中,由勾股定理求出
中,由勾股定理求出![]() ,得出
,得出![]() ;在
;在![]() 中,由勾股定理得出方程,解方程得出
中,由勾股定理得出方程,解方程得出![]() 即可;
即可;
②当点![]() 与点
与点![]() 重合时,点
重合时,点![]() 离点
离点![]() 最近,由①知,此时
最近,由①知,此时![]() ;当点
;当点![]() 与点
与点![]() 重合时,点
重合时,点![]() 离点
离点![]() 最远,此时四边形
最远,此时四边形![]() 为正方形,
为正方形,![]() ,
,![]() 即可得出答案.
即可得出答案.
(1)证明:![]() 折叠纸片使
折叠纸片使![]() 点落在边
点落在边![]() 上的
上的![]() 处,折痕为
处,折痕为![]() ,
,
![]() 点
点![]() 与点
与点![]() 关于
关于![]() 对称,
对称,
![]() ,
,![]() ,
,![]() .
.
又![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 为菱形.
为菱形.
(2)解:①![]() 四边形
四边形![]() 是矩形,
是矩形,
![]() ,
,![]() ,
,![]() .
.
![]() 点
点![]() 与点
与点![]() 关于
关于![]() 对称,
对称,
![]() .
.
在![]() 中,
中,
![]() ,
,
![]() .
.
在![]() 中,
中,
![]() ,
,![]() ,
,
![]() .
.
解得,![]() .
.
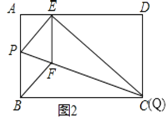
②当点![]() 与点
与点![]() 重合时,点
重合时,点![]() 离点
离点![]() 最近,如图
最近,如图![]() ,由①知,此时
,由①知,此时![]() .
.
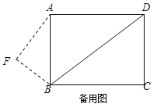
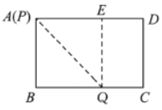
当点![]() 与点
与点![]() 重合时,点
重合时,点![]() 离点
离点![]() 最远,如下图:此时四边形
最远,如下图:此时四边形![]() 为正方形,
为正方形,![]() ,
,
![]() 点
点![]() 在边
在边![]() 上移动的最大距离为
上移动的最大距离为![]() .
.

练习册系列答案
相关题目