题目内容
【题目】如图,已知∠AOB=120°,射线OA绕点O以每秒钟6°的速度逆时针旋转到OP,设射线OA旋转OP所用时间为t秒(t<30).
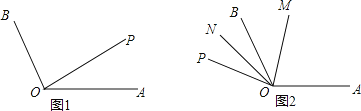
(1)如图1,直接写出∠BOP= °(用含t的式子表示);
(2)若OM平分∠AOP,ON平分∠BOP.
①当OA旋转到如图1所示OP处,请完成作图并求∠MON的度数;
②当OA旋转到如图2所示OP处,若2∠BOM=3∠BON,求t的值.
【答案】(1)(120﹣6t);(2)①60°;②t=28
【解析】
试题分析:(1)由于∠AOB=120°,∠AOP=6t,即可得到∠BOP=(120﹣6t)°;
(2)根据角平分线的定义得到∠MOP=![]() ∠AOP=3t,∠NOP=
∠AOP=3t,∠NOP=![]() ∠BOP=60﹣3t,根据线段的和差即可得到结论;
∠BOP=60﹣3t,根据线段的和差即可得到结论;
(3)根据角平分线的定义得到∠MOA=∠MOP=![]() ∠AOP=3t,∠BON=∠NOP=
∠AOP=3t,∠BON=∠NOP=![]() ∠BOP=3t﹣60,根据已知条件列方程即可得到结论.
∠BOP=3t﹣60,根据已知条件列方程即可得到结论.
解:(1)∵∠AOB=120°,∠AOP=6t,
∴∠BOP=(120﹣6t)°.
故答案为:(120﹣6t);
(2)∵OM平分∠AOP,ON平分∠BOP,
∴∠MOP=![]() ∠AOP=3t,∠NOP=
∠AOP=3t,∠NOP=![]() ∠BOP=60﹣3t,
∠BOP=60﹣3t,
∴∠MON=∠MOP+∠NOP=3t+60﹣3t=60°;
(3)∵OM平分∠AOP,ON平分∠BOP,
∴∠MOA=∠MOP=![]() ∠AOP=3t,
∠AOP=3t,
∠BON=∠NOP=![]() ∠BOP=3t﹣60,
∠BOP=3t﹣60,
∵2∠BOM=3∠BON,
即2(120﹣3t)=3(3t﹣60),
解得t=28.

练习册系列答案
相关题目