题目内容
【题目】已知,在平面直角坐标系中,点A(2015,0)、B(0,2013),以AB为斜边在直线AB下方作等腰直角△ABC,则点C的坐标为 .
【答案】(1,﹣1).
【解析】
试题分析:如图设△CAB是等腰直角三角形,点C坐标(x,y),作CE⊥OA于E,CF⊥OB于F,先证明△ACE≌△BCF,推出四边形OECF是正方形,列出方程即可解决问题.
解:如图设△CAB是等腰直角三角形,点C坐标(x,y),作CE⊥OA于E,CF⊥OB于F.
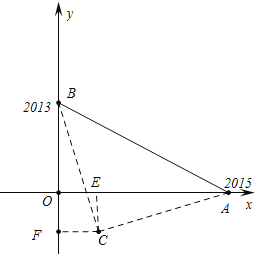
∵∠CEO=∠CFO=∠EOF=90°.
∴四边形OECF是矩形,
∴CE=OF,PF=OE,∠ECF=90°,
∵∠ECF=∠ACB=90°,
∴∠ACE=∠BCF,
在△ACE和△BCF中,
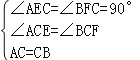 ,
,
∴△ACE≌△BCF,
∴CE=CF,AE=BF,
∴四边形OECF是正方形,
∴x=﹣y,2013+x=2015﹣x,
∴x=1,y=﹣1,
∴点C坐标(1,﹣1).
故答案为(1,﹣1).

练习册系列答案
相关题目