题目内容
【题目】如图所示,抛物线y=x2﹣4x+3与x轴分别交于A、B两点,交y轴于点C,
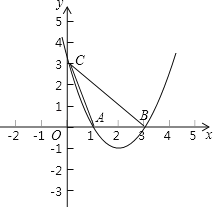
(1)求cos∠CAO的值;
(2)求直线AC的函数关系式;
(3)如果有动点P是y轴上,且△OPA与△OAC相似,求P点坐标.
【答案】(1)cos∠CAO=![]() ;(2)直线AC的解析式为:y=﹣3x+3;(3)点P的坐标为:(0,﹣3),(0,
;(2)直线AC的解析式为:y=﹣3x+3;(3)点P的坐标为:(0,﹣3),(0,![]() ),(0,﹣
),(0,﹣![]() ).
).
【解析】
试题分析:(1)根据抛物线y=x2﹣4x+3与x轴分别交于A、B两点,交y轴于点C,可以求得A、B、C三点的坐标,从而可以求得OA、OC、AC的长,进而可以得到cos∠CAO的值;
(2)根据点A、C两点的坐标,可以求得直线AC的函数关系式;
(3)根据第三问的条件,可知符合要求的三角形OPA存在三种情况,然后分别画出相应的图形,即可求得点P的坐标.
解:(1)∵抛物线y=x2﹣4x+3与x轴分别交于A、B两点,交y轴于点C,
∴x2﹣4x+3=0,得x=1或x=3,x=0时,y=3,
∴点A的坐标为(1,0),点B的坐标为(3,0),点C的坐标为(0,3),
∴OA=1,OC=3,
∴![]() ,
,
∴cos∠CAO=![]() ;
;
(2)设直线AC的解析式为:y=kx+b,
∵点A的坐标为(1,0),点C的坐标为(0,3),
∴![]()
解得k=﹣3,b=3.
即直线AC的解析式为:y=﹣3x+3;
(3)如果有动点P是y轴上,且△OPA与△OAC相似,
则有如下三种情况,
第一种情况如下图1所示,
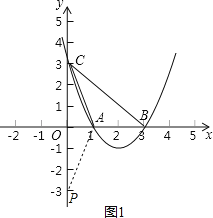
当∠OPA=∠OCA,∠AOC=∠AOP时,△OPA∽△OAC,
∴![]() ,
,
∵点C的坐标为(0,3),
∴OP=OC=3,
∴点P的坐标为(0,﹣3);
第二种情况如下图2所示,点P位于y轴正半轴,
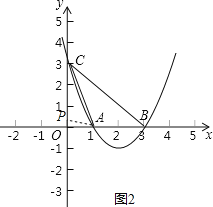
当∠OPA=∠OAC,∠AOC=∠AOP时,△OPA∽△OAC,
∴![]() ,
,
∵点C的坐标为(0,3),点A的坐标为(1,0),
∴OA=1,OC=3,
∴![]() ,
,
即点P的坐标为(0,![]() );
);
第三种情况如下图3所示,点P位于y轴负半轴,
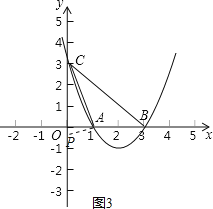
当∠OPA=∠OAC,∠AOC=∠AOP时,△OPA∽△OAC,
∴![]() ,
,
∵点C的坐标为(0,3),点A的坐标为(1,0),
∴OA=1,OC=3,
∴![]() ,
,
即点P的坐标为(0,﹣![]() ).
).
由上可得,点P的坐标为:(0,﹣3),(0,![]() ),(0,﹣
),(0,﹣![]() ).
).