题目内容
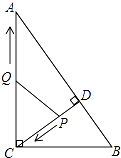
【题目】如图,在正方形ABCD中,AB=4,P是CD边上的动点(P点不与C、D重合),过点P作直线与BC的延长线交于点E,与AD交于点F,且CP=CE,连接DE、BP、BF,设CP=x,△PBF的面积为S1,△PDE的面积为S2
(1)求证:BP⊥DE;
(2)求S1﹣S2关于x的函数解析式,并写出x的取值范围;
(3)当∠PBF=30°时,求S1﹣S2的值.
【答案】(1)见解析;(2)S1﹣S2=8﹣2x(0<x<4);(3)S1﹣S2=8﹣2x=8﹣![]() .
.
【解析】
(1)如图1中,延长BP交DE于M.只要证明△BCP≌△DCE,推出∠BCP=∠CDE,由∠CBP+∠CPB=90°,∠CPB=∠DPM,即可推出∠CDE+∠DPM=90°,延长即可解决问题;
(2)根据S1-S2=S△PBF-S△PDE计算即可解决问题;
(3)先求出PC的长,再利用(2)中结论计算即可;
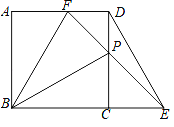
(1)如图1中,延长BP交DE于M.
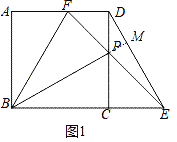
∵四边形ABCD是正方形,
∴CB=CD,∠BCP=∠DCE=90°,
∵CP=CE,
∴△BCP≌△DCE,
∴∠BCP=∠CDE,
∵∠CBP+∠CPB=90°,∠CPB=∠DPM,
∴∠CDE+∠DPM=90°,
∴∠DMP=90°,
∴BP⊥DE.
(2)由题意S1﹣S2=[16﹣2x﹣2x﹣![]() (4﹣x)2]﹣
(4﹣x)2]﹣![]() (4﹣x)x
(4﹣x)x
=8﹣2x(0<x<4).
(3)如图2中,
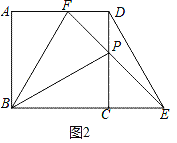
∵∠PBF=30°,
∵CP=CE,∠DCE=90°,
∴∠CPE=∠CEP=∠DPF=45°,∠FDP=90°,
∴∠PFD=∠DPF=45°,
∴DF=DP,∵AD=CD,
∴AF=PC,∵AB=BC,∠A=∠BCP=90°,
∴△BAF≌△BCP,
∴∠ABF=∠CBP=30°,
∴x=PC=BCtan30°=![]() ,
,
∴S1﹣S2=8﹣2x=8﹣![]()