题目内容
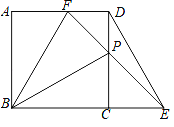
【题目】如图,两张宽为1cm的矩形纸条交叉叠放,其中重叠部分部分是四边形ABCD, 
(1)试判断四边形ABCD的形状,并说明理由
(2)若∠BAD=30°,求重叠部分的面积.
【答案】
(1)解:四边形ABCD是菱形,
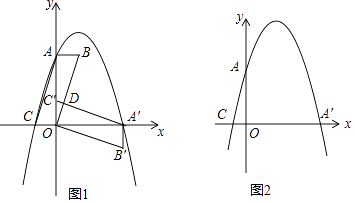
理由是:如图1所示:
∵依题意可知AB∥CD,AD∥BC,
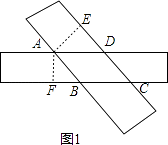
∴四边形ABCD是平行四边形,
分别作CD,BC边上的高为AE,AF,
∵两纸条相同,
∴纸条宽度AE=AF,
∵平行四边形的面积为AE×CD=BC×AF,
∴CD=BC,
∴平行四边形ABCD为菱形
(2)解:如图2所示,过B、D两点分别作BE⊥AD、DF⊥AB,垂足分别为E、F, 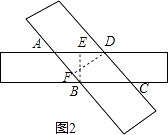
∵宽为1cm,
∴BE=DF=1cm,
∵∠BAD=30°,
∴AB=2cm,
∴重叠部分的面积为DF×B=1×2=2cm2
【解析】(1)考查菱形的判定,四条边相等的四边形即为菱形;(2)要求重叠部分的面积,根据面积公式,求出底和高即可.可以通过作辅助线求得.

练习册系列答案
相关题目
【题目】请你用学习“一次函数”时积累的经验和方法解决下列问题:
(1)在平面直角坐标系中,画出函数y=|x|的图象;
①列表填空:
x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
y | … | … |
②描点、连线,在图所示的平面直角坐标系中画出y=|x|的图象;
(2)结合所画函数图象,写出y=|x|的两条不同类型的性质.