题目内容
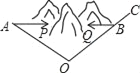
【题目】某工程队准备开挖一条隧道,为了缩短工期,必须在山的两侧同时开挖,为了确保两侧开挖的隧道在同一条直线上,测量人员在如图所示的同一高度定出了两个开挖点P和Q,然后在左边定出开挖的方向线AP,为了准确定出右边开挖的方向线BQ,测量人员取一个可以同时看到点A,P,Q的点O,测得∠A=28°,∠AOC=100°,那么∠QBO应等于多少度才能确保BQ与AP在同一条直线上?
【答案】∠QBO应等于52°才能确保BQ与AP在同一条直线上.
【解析】
当点A、P、Q、B共线时,即点P、Q在△OAB的边AB上,两侧开挖的隧道在同一条直线上,根据三角形内角和定理进行求解即可得.
当点A、P、Q、B共线时,即点P、Q在△OAB的边AB上,两侧开挖的隧道在同一条直线上,
∵∠A+∠B+∠AOB=180°,
∴∠B=180°﹣28°﹣100°=52°,
即∠QBO应等于52°才能确保BQ与AP在同一条直线上.

练习册系列答案
相关题目
【题目】请你用学习“一次函数”时积累的经验和方法解决下列问题:
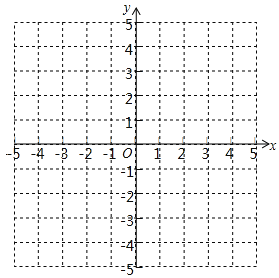
(1)在平面直角坐标系中,画出函数y=|x|的图象;
①列表填空:
x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
y | … | … |
②描点、连线,在图所示的平面直角坐标系中画出y=|x|的图象;
(2)结合所画函数图象,写出y=|x|的两条不同类型的性质.