Question

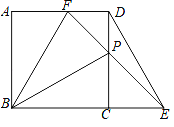
【题目】如图，在△ABC中，∠C=90°，点E，F分别在边AB，BC上，沿直线EF将△EBF翻折，使顶点B的对应点B1落在AC边上，且EB1⊥AC．求证：四边形BFB1E是菱形．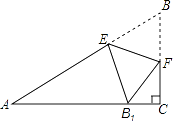

Answer 1

【答案】证明：∵∠C=90°， ∴AC⊥BC，
∵EB1⊥AC，
∴EB1∥BC，
由折叠的性质得：BE1=BE，∠EB1F=∠B，
∵∠A+∠B=90°，∠EB1F+∠FB1C=90°，
∴∠A=∠FB1C，
∴AB∥B1F，
∴四边形四边形BFB1E是平行四边形，
又∵BE1=BE，
∴四边形BFB1E是菱形．
【解析】首先证出EB1∥BC，由折叠的性质得：BE1=BE，∠EB1F=∠B，由角的互余关系证出∠A=∠FB1C，得出AB∥B1F，证出四边形四边形BFB1E是平行四边形，即可得出四边形BFB1E是菱形．
【考点精析】关于本题考查的菱形的判定方法和翻折变换（折叠问题），需要了解任意一个四边形，四边相等成菱形；四边形的对角线，垂直互分是菱形．已知平行四边形，邻边相等叫菱形；两对角线若垂直，顺理成章为菱形；折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等才能得出正确答案．