题目内容
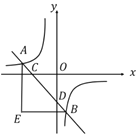
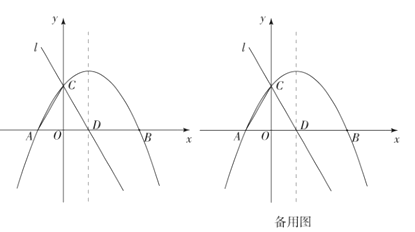
【题目】抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,且顶点在
,且顶点在![]() 轴上,与
轴上,与![]() 轴的交点为
轴的交点为![]() ,
,![]() 点的坐标为
点的坐标为![]() ,点
,点![]() 在抛物线的对称轴上,直线
在抛物线的对称轴上,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() .
.
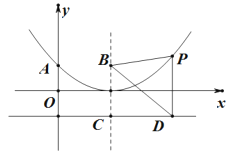
(1)求该抛物线的函数表达式.
(2)点![]() 是(1)中图象上的点,过点
是(1)中图象上的点,过点![]() 作
作![]() 轴的垂线与直线
轴的垂线与直线![]() 交于点
交于点![]() .试判断
.试判断![]() 是否为等腰三角形,并说明理由.
是否为等腰三角形,并说明理由.
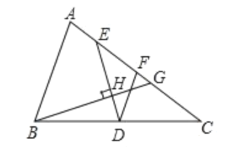
(3)作![]() 于点
于点![]() ,当点
,当点![]() 从横坐标2013处运动到横坐标2019处时,请求出点
从横坐标2013处运动到横坐标2019处时,请求出点![]() 运动的路径长.
运动的路径长.
【答案】(1)抛物线的函数表达式为![]() ;(2)
;(2)![]() 是等腰三角形,理由见解析;(3)点
是等腰三角形,理由见解析;(3)点![]() 的运动路径长为3.
的运动路径长为3.
【解析】
(1)由题意可知抛物线的顶点坐标,进而可设抛物线的顶点表达式,再将点A坐标代入计算即可;
(2)设点![]() 的坐标为
的坐标为![]() ,则
,则![]() ,利用勾股定理可求得PB长,再利用P、D坐标可求得PD长,进而证得
,利用勾股定理可求得PB长,再利用P、D坐标可求得PD长,进而证得![]() 是等腰三角形;
是等腰三角形;
(3)设直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,则
,则![]() ,先证得
,先证得![]() 是
是![]() 的中位线,进而可知点
的中位线,进而可知点![]() 在
在![]() 轴上运动,再通过点P横坐标的变化可求得CD的长度变化,进而求得点E的路径长.
轴上运动,再通过点P横坐标的变化可求得CD的长度变化,进而求得点E的路径长.
(1)根据题意得抛物线的顶点坐标为![]() ,
,
所以设抛物线的函数表达式为![]() ,
,
把点![]() 的坐标代入得:
的坐标代入得:![]() ,解得
,解得![]() ,
,
∴抛物线的函数表达式为![]()
(2)![]() 是等腰三角形;
是等腰三角形;
理由:设点![]() 的坐标为
的坐标为![]() ,则点D坐标为
,则点D坐标为![]() ,
,
∵点![]() 的坐标为
的坐标为![]() ,点B坐标为
,点B坐标为![]() ,
,
∴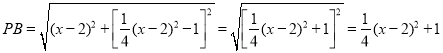 ,
,
∵点![]() 的坐标为
的坐标为![]() ,点D坐标为
,点D坐标为![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是等腰三角形;
是等腰三角形;
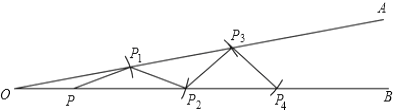
(3)如图所示:

∵![]() ,
,![]() ,
,
∴![]() ,
,
即点E为BD中点,
设直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,则
,则![]() ,
,
∴![]() ,
,
∴点F为BC中点,
∴![]() 是
是![]() 的中位线,
的中位线,
∴![]() ,
,![]() ,
,
∴点![]() 在
在![]() 轴上运动,
轴上运动,
∴当![]() 的横坐标为2013时,
的横坐标为2013时,![]() ,此时
,此时![]() ,
,
当![]() 的横坐标为2019时,
的横坐标为2019时,![]() ,此时
,此时![]() ,
,
∴点![]() 的运动路径长为:
的运动路径长为:![]() .
.

【题目】九年级某班组织班级联欢会,最后进入抽奖环节,每名同学都有一次抽奖机会.抽奖方案如下:将一副扑克牌中点数为“2”、“3”、“3”、“5”、“6”的五张牌背面朝上洗匀,先从中抽出1张牌,再从余下的4张牌中抽出1张牌,记录两张牌点数后放回,完成一次抽奖.记每次抽出两张牌点数之差为![]() ,按下表要求确定奖项.
,按下表要求确定奖项.
奖项 | 一等奖 | 二等奖 | 三等奖 |
|
|
|
|
(1)用列表法或画树状图的方法求出甲同学获二等奖的概率;
(2)判断是否每次抽奖都会获奖?请说明理由.
【题目】某校为了解八年级学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知![]() .
.![]() 两组发言人数的比为
两组发言人数的比为![]() ,请结合图中相关数据回答下列问题:
,请结合图中相关数据回答下列问题:
发言次数 | |
|
|
|
|
|
|
|
|
|
|
|
|
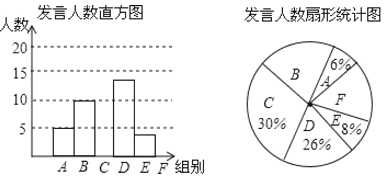
(1)求出样本容量,并补全直方图;
(2)该年级共有学生1500人,请估计全年级在这天里发言次数不少于12次的人数;
(3)已知![]() 组发言的学生中恰有1位男生,
组发言的学生中恰有1位男生,![]() 组发言的学生中有2位女生.现从
组发言的学生中有2位女生.现从![]() 组与
组与![]() 组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率
组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率