题目内容
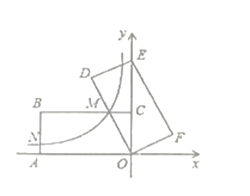
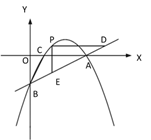
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图像交于
的图像交于![]() 、
、![]() ,与
,与![]() 轴、
轴、![]() 轴相交于
轴相交于![]() 、
、![]() 两点,过点
两点,过点![]() 、
、![]() 作
作![]() 轴、
轴、![]() 轴平行线交于点
轴平行线交于点![]() ,若
,若![]() ,
,![]() ,则
,则![]() __________.
__________.
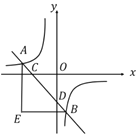
【答案】![]()
【解析】
先通过求点C、D坐标得到△COD为等腰直角三角形,进而通过△COD的面积求得一次函数关系式,再通过过点![]() 、
、![]() 作
作![]() 轴、
轴、![]() 轴平行线交于点
轴平行线交于点![]() 证得△AEB为等腰直角三角形,利用△AEB的面积求得AE、BE的长,设点A坐标为(m,n),表示出点B坐标,再将点A、B坐标代入反比例函数关系式得到m与n的一个方程,再把点A代入一次函数关系式,得到一个m与n的方程,联立方程组求解即可.
证得△AEB为等腰直角三角形,利用△AEB的面积求得AE、BE的长,设点A坐标为(m,n),表示出点B坐标,再将点A、B坐标代入反比例函数关系式得到m与n的一个方程,再把点A代入一次函数关系式,得到一个m与n的方程,联立方程组求解即可.
解:∵直线![]() ,
,
∴当x=0时,y=b;当y=0时,x=b,
∴C(b,0),D(0,b)
∴OC=OD=-b,
∴△COD为等腰直角三角形,∠OCD=∠ODC=45°,
∵![]() ,
,
∴![]() ,解得
,解得![]() (舍正)
(舍正)
∴直线![]() ,
,
∵过点![]() 、
、![]() 作
作![]() 轴、
轴、![]() 轴平行线交与点
轴平行线交与点![]() ,
,
∴∠EAB=∠ODC=45°,∠EBA=∠OCD=45°,
∴∠EAB=∠EBA=45°,
∴EA=EB,∠E=90°,
∵![]() ,
,
∴![]() ,解得
,解得![]() (舍负),
(舍负),
设点A为(m,n),则点B为(m+![]() ,n-
,n-![]() ),
),
将点A、B代入![]() 得
得![]() ,
,
整理得![]() ①,
①,
将点A代入![]() 得
得![]() ②,
②,
将①②联立方程组,解得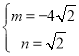 ,
,
∴![]() ,
,
故答案为:![]()

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目