题目内容
如图,AD⊥BC于D,AD=BD,AC=BE.
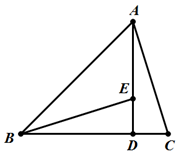
(1)证明∠BED=∠C ;
(2)证明:BE⊥AC.

(1)证明∠BED=∠C ;
(2)证明:BE⊥AC.
见解析
(1)利用垂直的性质可以得到∠BDE=∠ADC=90°,从而利用直角三角形的判定方法判定两个直角三角形全等,进而证得结论;
(2)延长BE交AC于点F,根据证得的直角三角形的对应边相等可以得到∠BED=∠C=∠AEF,从而利用∠AFE=180°-(∠DAC+∠AEF)=90°,进而证得BE⊥AC.
(2)延长BE交AC于点F,根据证得的直角三角形的对应边相等可以得到∠BED=∠C=∠AEF,从而利用∠AFE=180°-(∠DAC+∠AEF)=90°,进而证得BE⊥AC.

练习册系列答案
相关题目