题目内容
若等腰三角形腰上的高是腰长的一半,则这个等腰三角形的底角是
| A．75°或15° | B．75° | C．15° | D．75°和30° |
A
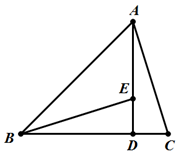
当等腰三角形是锐角三角形时，如图1所示
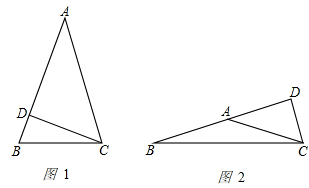
∵CD⊥AB，CD=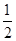
AC
∴sin∠A=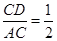
∴∠A=30°
∴∠B=∠ACB=75°
当等腰三角形是钝角三角形时，如图2示，
∵CD⊥AB，即在直角三角形ACD中，CD=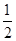AC
∴∠CAD=30°
∴∠CAB=150°
∴∠B=∠ACB=15°
故其底角为15°或75°
故选A
∵CD⊥AB，CD=
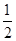AC∴sin∠A=
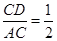
∴∠A=30°
∴∠B=∠ACB=75°
当等腰三角形是钝角三角形时，如图2示，
∵CD⊥AB，即在直角三角形ACD中，CD=
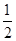AC∴∠CAD=30°
∴∠CAB=150°
∴∠B=∠ACB=15°
故其底角为15°或75°
故选A
练习册系列答案
期末复习检测系列答案
超能学典单元期中期末专题冲刺100分系列答案
黄冈360度定制密卷系列答案
阳光考场单元测试卷系列答案
相关题目
