题目内容
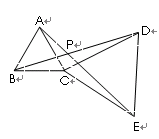
如图,BE、CF分别是 △ABC的边AC、AB上的高,且BP=AC,CQ=AB,求证:(1)AP=AQ;(2)AP⊥AQ

见解析
本题考查了三角形全等的判定和性质
(1)AC⊥BE,AB⊥QC可得∠FBP=∠ECP,再有BP=AC,CQ=AB,根据SAS证得△QAC≌△APB即可;
(2)由△APB≌△QAC,得∠BAP=∠CQA,通过等量代换得∠BAP+∠QAF=90°即可得AP⊥AQ.
(1)证明:∵AC⊥BE,AB⊥QC (2)∵△QAC≌△APB
∴∠BFP=∠CEP=90° ∴∠AQF=∠PAF
又∵∠FBP=∠EPC 又AB⊥QC
∴∠FBP=∠ECP ∴∠QFA=90°
在△QAC的△APB中 ∴∠FQA+∠FAQ=90°
BP=AC ∴∠FQA+∠PAF=90°
∠FBP=∠ECP 即∠PAQ=90°
CQ=AB ∴AP⊥AQ
∴△QAC≌△APB(SAS)
∴AP=AQ
(1)AC⊥BE,AB⊥QC可得∠FBP=∠ECP,再有BP=AC,CQ=AB,根据SAS证得△QAC≌△APB即可;
(2)由△APB≌△QAC,得∠BAP=∠CQA,通过等量代换得∠BAP+∠QAF=90°即可得AP⊥AQ.
(1)证明:∵AC⊥BE,AB⊥QC (2)∵△QAC≌△APB
∴∠BFP=∠CEP=90° ∴∠AQF=∠PAF
又∵∠FBP=∠EPC 又AB⊥QC
∴∠FBP=∠ECP ∴∠QFA=90°
在△QAC的△APB中 ∴∠FQA+∠FAQ=90°
BP=AC ∴∠FQA+∠PAF=90°
∠FBP=∠ECP 即∠PAQ=90°
CQ=AB ∴AP⊥AQ
∴△QAC≌△APB(SAS)
∴AP=AQ

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
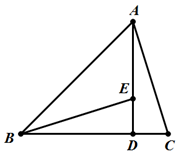
 ,∠B=
,∠B= ,BC=4,则AB=_____.
,BC=4,则AB=_____.
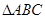 中,D是AB边上的动点,以CD为一边,向上作等边
中,D是AB边上的动点,以CD为一边,向上作等边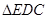 ,连结AE。
,连结AE。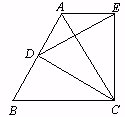
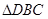 和
和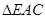 会全等吗?请说说你的理由。
会全等吗?请说说你的理由。