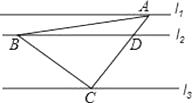
题目内容
【题目】问题:已知△ABC中,∠ABC=∠ACB=α,点D是AB边上任意一点,连结CD,在CD的上测作以CD为底边,α为底角的等腰△CDE,连结AE,试探究BD与AE的数量关系.
(1)尝试探究如图1,当α=60°时,小聪同学猜想有BD=AE,以下是他的思路呈现.请你根据他的思路把这个证明过程完整地表达出来;

(2)特例再探如图2,当α=45°时,请你判断线段BD与AE之间的数量关系,并进行证明;
(3)问题解决如图3,当α为任意锐角时,请直接写出线段BD与AE的数量关系是 . (用含α的式子表示,其中0°<α<90°)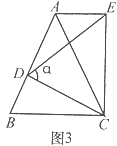
【答案】
(1)
解:BD=AE;∵∠BCA=60°,∠DCE=60°,
∴∠BCD=∠ACE,
在△BDC与△AEC中,  ,
,
∴△BDC≌△AEC,
∴BD=AE
(2)
解:BD= ![]() AE;理由如下:
AE;理由如下:
过点D作DF∥AC,交BC于F.
∵DF∥AC,
∴∠ABC=∠DFB.
∵∠ABC=∠ACB=α,α=45°,
∴∠ABC=∠ACB=∠DFB=45°.
∴△DFB是等腰直角三角形
∴BD=DF= ![]() BF.
BF.
∵AE∥BC,
∴∠ABC+∠BAE=180°.
∵∠DFB+∠DFC=180°
∴∠BAE=∠DFC.
∵∠ABC+∠BCD=∠ADC,∠ABC=∠CDE=α,
∴∠ADE=∠BCD.
∴△ADE∽△FCD.
∴ ![]() =
= ![]() .
.
∵DF∥AC,
∴ ![]() =
= ![]() .
.
∴ ![]() =
= ![]() =
= ![]() ,
,
∴BD= ![]() AE
AE
(3)BD=2cosα?AE
【解析】解(3)∵∠ABC=∠ACB=∠EDC=∠ECD=α,
∴∠BCD=∠ACE,
∵∠ADE+∠EDC=∠B+∠BCD,
∴∠ADE=∠ACE,
∴A、D、C、E四点共圆,
∴∠ADE=∠BCD=∠ACE,∠ABC=∠ACB=α,
∴△BDC∽△ACE,
∴ ![]() =
= ![]() ,
,
又∵ ![]() =cosα,
=cosα,
∴BD=2cosαAE.
所以答案是:BD=2cosαAE.