Question

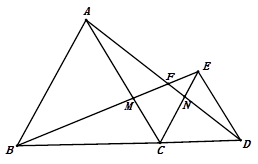
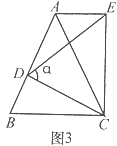
【题目】如图，已知抛物线y=﹣x2+3x与x轴的正半轴交于点A，点B在抛物线上，且横坐标为2，作BC⊥x轴于点C，⊙B经过原点O，点E为⊙B上一动点，点F在AE上．

（1）求点A的坐标；
（2）如图1，连结OE，当AF：FE=1：2时，求证：△ACF∽△AOE；
（3）如图2，当点F是AE的中点时，求CF的最大值．

Answer 1

【答案】
（1）解：令y=0，则﹣x2+3x=0，

解得x1=0，x2=3，

则A（3，0）

（2）解：如图1，

当x=2时，y=﹣22+3×2=2，

∴B（2，2）．

∵BC⊥OA，

∴OC=2，AC=OA﹣OC=1．

∵AF：FE=1：2，

∴ = = ．

∵∠CAF=∠OAE，

∴△ACF∽△AOE

（3）解：取OC的中点D，连接DE，BD，BE，BO，如图2，

则有OD=DC=1，BD= = ，BE=BO= =2

根据两点之间线段最短可得：

DE≤BD+BE= +2 ．

∵AC=DC=1，AF=EF，

∴CF= DE≤ ，

∴CF的最大值为 ．

【解析】（1）只需令y=0，就可求出点A的坐标；（2）由于∠CAF=∠OAE，要证△ACF∽△AOE，只需证 = ，只需求出点B的坐标就可解决问题；（3）由点F是AE的中点，联想到三角形中位线定理，取OC的中点D，连接DE，BD，BE，BO，如图2，则有CF= DE，要求CF的最大值，只需求DE的最大值，只需运用两点之间线段最短就可解决问题．
【考点精析】通过灵活运用线段的基本性质和勾股定理的概念，掌握线段公理：所有连接两点的线中，线段最短．也可简单说成：两点之间线段最短；连接两点的线段的长度，叫做这两点的距离；线段的大小关系和它们的长度的大小关系是一致的；直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2即可以解答此题．