题目内容
【题目】如图,直线l1∥l2∥l3 , 等腰Rt△ABC的三个顶点A,B,C分别在l1 , l2 , l3上,∠ ACB=90°,AC交l2于点D,已知l1与l2的距离为1,l2与l3的距离为3,则AB:BD的值为( ) 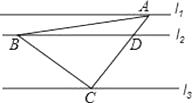
A.![]()
B.![]()
C.![]()
D.![]()
【答案】A
【解析】解:如图,过点B作BF![]() l3于点F,过点A作AE
l3于点F,过点A作AE![]() l3于点E,
l3于点E,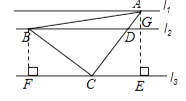
∵![]() ACB=90
ACB=90![]() ,
,
∴![]() BCF+
BCF+![]() ACE=90
ACE=90![]() ,
,
∵![]() BCF+
BCF+![]() CFB=90
CFB=90![]() ,
,
∴![]() ACE=
ACE=![]() CBF,
CBF,
在![]() ACE和
ACE和![]() CBF中,
CBF中,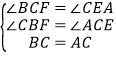 ,
,
∴![]() ACE
ACE![]()
![]() CBF,
CBF,
∴CE=BF=3,CF=AE=4,
∵l1与l2的距离为1,l2与l3的距离为3,
∴AG=1,BG=EF=CF+CE=7,
∴AB=![]() =
=![]() ,
,
∵l2∥l3 ,
∴![]() ,
,
∴DG=![]() CE=
CE=![]() ,
,
∴BD=BG-DG=7-![]() =
=![]() ,
,
∴![]() .
.
故选A.
【考点精析】本题主要考查了平行线分线段成比例的相关知识点,需要掌握三条平行线截两条直线,所得的对应线段成比例才能正确解答此题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目