题目内容
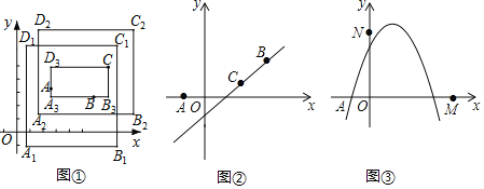
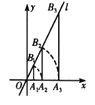
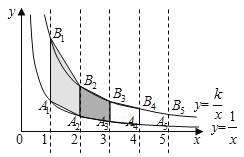
【题目】在滑草过程中,小明发现滑道两边形如两条双曲线,如图,点A1,A2,A3…在反比例函数y=![]() (x>0)的图象上,点B1,B2,B3…反比例函数y=
(x>0)的图象上,点B1,B2,B3…反比例函数y=![]() (k>1,x>0)的图象上,A1B1∥A2B2…∥y轴,已知点A1,A2…的横坐标分别为1,2,…,令四边形A1B1B2A2、A2B2B3A3、…的面积分别为S1、S2、….若S19=39,则k=__.
(k>1,x>0)的图象上,A1B1∥A2B2…∥y轴,已知点A1,A2…的横坐标分别为1,2,…,令四边形A1B1B2A2、A2B2B3A3、…的面积分别为S1、S2、….若S19=39,则k=__.
【答案】761
【解析】
根据反比例函数图象上点的特征和平行于y轴的直线的性质计算A1B1、A2B2、…,最后根据梯形面积公式可得S1、S2、S3、…Sn的值并找规律,根据已知S19=39列方程可得k的值.
解:∵A1B1//A2B2…//y轴,
∴A1和B1的横坐标相等,A2和B2的横坐标相等,…,An和Bn的横坐标相等,
∵点A1,A2…的横坐标分别为1,2,…,
∴点B1,B2…的横坐标分别为1,2,…,
∵点A1,A2,A3…在反比例函数y=![]() (x>0)的图象上,点B1,B2,B3…反比例函数y=
(x>0)的图象上,点B1,B2,B3…反比例函数y=![]() (k>1,x>0)的图象上,
(k>1,x>0)的图象上,
∴A1B1=k-1,A2B2=![]() ,
,
∴S1=![]() ×1×(
×1×(![]() -
-![]() +k-1)=
+k-1)=![]() (
(![]() k-
k-![]() )=
)=![]() ,
,
同理得:A3B3=![]() -
-![]() =
=![]() ,A4B4=
,A4B4=![]() ,…,
,…,
∴S2=![]() =
=![]() (k-1),
(k-1),
S3=![]() =
=![]() (k-1),
(k-1),
…,
∴Sn=![]() ,
,
∵S19=39,
∴![]() ×(k-1)=39,
×(k-1)=39,
解得:k=761,
故答案为:761.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目