题目内容
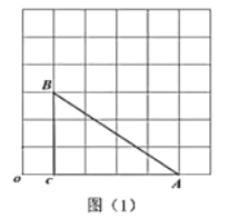
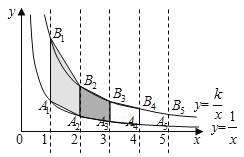
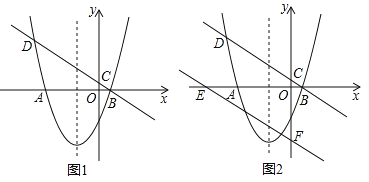
【题目】在平面直角坐标系中,对于任意三点A,B,C,给出如下定义:若矩形的任何一条边均与某条坐标轴平行或重合,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的外延矩形,点A,B,C的所有外延矩形中,面积最小的矩形称为点A,B,C的最佳外延矩形.例如,图①中的矩形A1B1C1D1,A2B2C2D2,A3B3CD3,都是点A,B,C的外延矩形,矩形A3B3CD3是点A,B,C的最佳外延矩形.
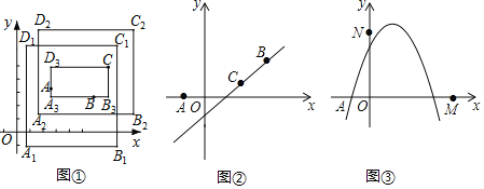
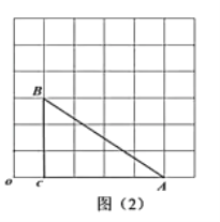
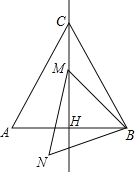
(1)如图②,已知A(﹣1,0),B(3,2),点C在直线y=x﹣1上,设点C的横坐标为t.
①若t=![]() ,则点A,B,C的最佳外延矩形的面积为多少?
,则点A,B,C的最佳外延矩形的面积为多少?
②若点A,B,C的最佳外延矩形的面积为9,求t的值.
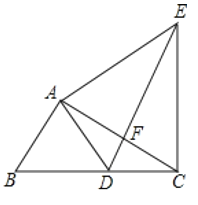
(2)如图③,已知点M(4,0),N(0,![]() ),P(x,y)是抛物线y=﹣x2+2x+3上一点,求点M,N,P的最佳外延矩形面积的最小值,以及此时点P的横坐标x的取值范围;
),P(x,y)是抛物线y=﹣x2+2x+3上一点,求点M,N,P的最佳外延矩形面积的最小值,以及此时点P的横坐标x的取值范围;
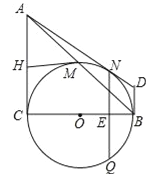
(3)已知D(1,0).若Q是抛物线y=﹣x2﹣2mx﹣m2+2m+1的图象在﹣2≤x≤1之间的最高点,点E的坐标为(0,4m),设点D,E,Q的最佳外延矩形的面积为S,当4≤S≤6时,直接写出m的取值范围.
【答案】(1)①8;②t的值为![]() 或
或![]() ;(2)最小值为14,此时P点横坐标x的取值范围为:0≤x≤1﹣
;(2)最小值为14,此时P点横坐标x的取值范围为:0≤x≤1﹣![]() 或1+
或1+![]() ≤x≤3;(3)m的取值范围为:
≤x≤3;(3)m的取值范围为:![]() ≤m≤
≤m≤![]() 或﹣
或﹣![]() ≤m≤﹣1
≤m≤﹣1
【解析】
(1)①以AB为对角线的矩形面积即为所求.
②分两种情况讨论:C在x轴下方;C在B点右上方.分别列方程求解即可.
(2)分别令y等于M、N的纵坐标,解出方程并结合图形即可得出答案.
(3)先求出抛物线的顶点坐标,然后讨论抛物线对称轴与所给的x的范围的关系,对于每一种情况,分别表示出S,再根据S的范围解不等式组即可求出m的取值范围.
(1)①如图②,作矩形ANBM,
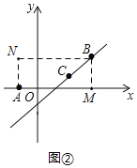
∵t=![]() ,∴C(
,∴C(![]() ,
,![]() ),
),
∵A(﹣1,0),B(3,2),∴C在矩形ANBM内部,
此时,矩形ANBM是点A,B,C的最佳外延矩形.
S矩形ANBM=AMBM=(3+1)(2﹣0)=8.
故答案为8.
②若C在x轴下方,则:4[2﹣(t﹣1)]=9,解得t=![]() .
.
若C在B点右上方,则:(t+1)(t﹣1)=9,解得t1=﹣![]() (舍),t2=
(舍),t2=![]() .
.
综上所述,t的值为![]() 或
或![]() .
.
(2)令y=﹣x2+2x+3=![]() ,解得x1=1+
,解得x1=1+![]() ,x2=1﹣
,x2=1﹣![]() ,
,
令y=﹣x2+2x+3=0,解得x1=﹣1,x2=3,
点M,N,P的最佳外延矩形面积的最小值为4×![]() =14,
=14,
此时P点横坐标x的取值范围为:0≤x≤1﹣![]() 或1+
或1+![]() ≤x≤3.
≤x≤3.
(3)∵y=﹣x2﹣2mx﹣m2+2m+1=﹣(x+m)2+2m+1,
∴抛物线的顶点坐标为(﹣m,2m+1).
①当1≤﹣m即m≤﹣1时,Q点坐标为(1,﹣m2)
若﹣m2<4m,则m>0(舍)或m<﹣4,此时S=m2,
∵4≤S≤6,∴﹣![]() ≤m≤﹣2(舍).
≤m≤﹣2(舍).
若﹣m2≥4m,则﹣4≤m≤0,此时S=﹣4m,
∴4≤﹣4m≤6,解得:﹣![]() ≤m≤﹣1,
≤m≤﹣1,
②当﹣2<﹣m<1即﹣1<m<2时,Q点的坐标就是抛物线顶点,S=4m(m+1),
∴4≤4m(m+1)≤6,解得![]() ≤m≤
≤m≤![]() ,
,
③当﹣m≤﹣2即m≥2时,4m≥8,不合题意,舍去.
综上所述,m的取值范围为:![]() ≤m≤
≤m≤![]() 或﹣
或﹣![]() ≤m≤﹣1.
≤m≤﹣1.

 名校课堂系列答案
名校课堂系列答案