题目内容
【题目】如图1,在平面直角坐标系中,![]() 为坐标原点.直线
为坐标原点.直线![]() 与抛物线
与抛物线![]() 同时经过
同时经过![]() .
.
(1)求![]() 的值.
的值.
(2)点![]() 是二次函数图象上一点,(点
是二次函数图象上一点,(点![]() 在
在![]() 下方),过
下方),过![]() 作
作![]()
![]() 轴,与
轴,与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .求
.求![]() 的最大值.
的最大值.
(3)在(2)的条件下,是否存在点![]() ,使
,使![]() 和
和![]() 相似?若存在,求出
相似?若存在,求出![]() 点坐标,不存在,说明理由.
点坐标,不存在,说明理由.
【答案】(1)m=1,n=3;(2)4;(3)N![]() 或N
或N![]() .
.
【解析】
(1)应用待定系数法求抛物线的解析式中的m和n的值;
(2)求出一次函数解析式,联系点的坐标的几何意义表示线段MN的长,根据所列关系式求最大值;
(3)分两种情况讨论,当![]() 时,得到
时,得到![]() ,计算OQ和NQ的值,得点N的坐标;当N为AB中点时,得到
,计算OQ和NQ的值,得点N的坐标;当N为AB中点时,得到![]() ∽
∽![]() ,进而得到点N的坐标.
,进而得到点N的坐标.
解:(1)![]() 抛物线
抛物线![]() 经过两点
经过两点![]() ,
,
∴ ,
,
解得:![]() ,
,
所以m的值为1,n的值为3,此时二次函数的表达式为![]() .
.
(2)把点A(0,3),点B(4,0)代入y=kx+b,得:
![]() ,
,
解得: ,
,
∴经过A、B两点的一次函数的解析式为![]() .
.
![]() ,
,
∵0≤x≤4,∴ 当![]() 时,
时,![]() 取得最大值为4.
取得最大值为4.
(3)存在.
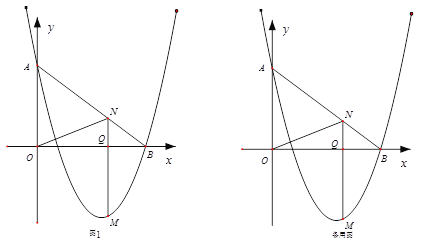
①当![]() 时,(如图1)
时,(如图1)

可证:![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵OA=3,OB=4,
∴AB=5,
∵ON·AB=OA·OB,
∴ON=![]() ,
,
∴NQ=![]() ,OQ=
,OQ=![]() ,
,
∴N![]() ;
;
②当N为AB中点时,(如图2)

![]() ,
,![]()
∴![]() ∽
∽![]() ,此时
,此时![]() .
.
∴满足条件的N![]() 或N
或N![]() .
.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案【题目】某校为了弘扬中华传统文化,了解学生整体阅读能力,组织全校的1000名学生进行一次阅读理解大赛.从中抽取部分学生的成绩进行统计分析,根据测试成绩绘制了频数分布表和频数分布直方图:
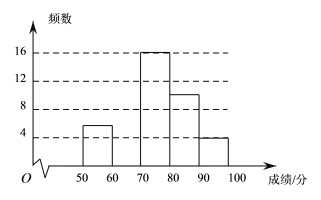
分组/分 | 频数 | 频率 |
50≤x<60 | 6 | 0.12 |
60≤x<70 |
| 0.28 |
70≤x<80 | 16 | 0.32 |
80≤x<90 | 10 | 0.20 |
90≤x≤100 | 4 | 0.08 |
(1)频数分布表中的![]() ;
;
(2)将上面的频数分布直方图补充完整;
(3)如果成绩达到90及90分以上者为优秀,可推荐参加决赛,估计该校进入决赛的学生大约有 人.