Question

【题目】如图，已知直线y＝﹣x+3交x轴于点A，交y轴于点B，抛物线y＝ax2+bx+c经过A、B、C（1，0）三点．

（1）求抛物线的解析式；

（2）观察图象，写出不等式ax2+bx+c＞﹣x+3的解集为　 　；

（3）若点D的坐标为（﹣1，0），在直线y＝﹣x+3上有一点P，使△ABO与△ADP相似，求出点P的坐标．

Answer 1

【答案】（1）y＝x2﹣4x+3；（2）x＜0或x＞3；（3）P1（﹣1，4），P2（1，2）．

【解析】

（1）根据题意首先利用交点式得出y＝a（x﹣1）（x﹣3），进而得出a的值即可；

（2）由题意直接利用函数图象得出ax2+bx+c＞﹣x+3的解集即为交点两侧两图象在上面的则对应函数值大，否则就小，进而得出答案；

（3）根据题意分析①若△ABO∽△AP1D，②若△ABO∽△ADP2，进而分别得出P点坐标即可．

解：（1）由题意得出：A（3，0），B（0，3），

∵抛物线y＝ax2+bx+c经过A、B、C（1，0）三点，

∴设y＝a（x﹣1）（x﹣3），（a≠0），

∴a×（﹣1）×（﹣3）＝3，

∴抛物线解析式为：y＝x2﹣4x+3；

（2）∵A（3，0），B（0，3），

∴利用图象可得出：不等式ax2+bx+c＞﹣x+3的解集为：x＜0或x＞3；

故答案为：x＜0或x＞3；

（3）由题意得：△ABO为等腰直角三角形，如图所示：

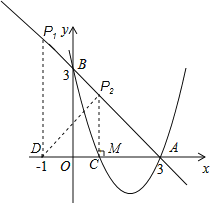
①若△ABO∽△AP1D，

则＝，

∴DP1＝AD＝4，

∴P1（﹣1，4）；

②若△ABO∽△ADP2，过点P2作P2M⊥x轴于点M，AD＝4，

∵△ABO为等腰直角三角形，

∴△ADP2是等腰直角三角形，由三线合一可得：DM＝AM＝2＝P2M，

∴MO＝1，

∴P2（1，2）．