Question

【题目】如图，等腰△ABC的顶角∠A＝36°，若将其绕点C顺时针旋转36°，得到△A′B′C，点B′在AB边上，A′B′交AC于E，连接AA′．有下列结论：①△ABC≌△A′B′C；②四边形A′ABC是平行四边形；③图中所有的三角形都是等腰三角形；其中正确的结论是（　　）

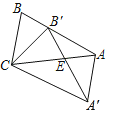
A.①②B.①③C.②③D.①②③

Answer 1

【答案】D

【解析】

由题意根据旋转不变性，等腰三角形的判定和性质，平行四边形的判定一一判断即可得到选项．

解：由旋转不变性可知：△ABC≌△A′B′C，故①正确，

∵AB＝AC，∠BAC＝36°，

∴∠B＝∠ACB＝72°，

∵CB＝CB′，

∴∠B＝∠CB′B＝72°，∠BCB′＝∠ACB′＝36°，

∴∠ACA′＝36°，

∴∠BAC＝∠ACA′，

∴AB∥A′C，

∵AB＝CA′，

∴四边形A′ABC是平行四边形，故②正确，

∵∠B＝∠BB′C＝72°，

∴△CBB′是等腰三角形，

∵∠EAB＝∠EB′A＝36°，

∴△EAB′是等腰三角形，

∵∠CB′E＝∠CEB′＝72°，

∴△CEB′是等腰三角形，

∵∠ECA′＝∠EA′C＝36°，

∴△ECA′是等腰三角形，

∵∠A′AE＝∠AEA′＝72°，

∴△A′AE是等腰三角形，

∴图中所有三角形都是等腰三角形，故③正确，

故选：D．