题目内容
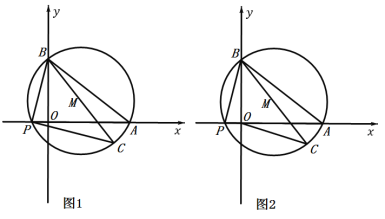
【题目】如图1,在平面直角坐标系中,点A、B的坐标分别为A(8,0)和B(0,6),点P为x轴负半轴上的一个动点,画△ABP的外接圆,圆心为M,连结BM并延长交圆于点C,连结CP.
(1)求证:.∠OBP=∠ABC
(2)当![]() 的直径为14时,求点P的坐标.
的直径为14时,求点P的坐标.
(3)如图2,连结OC,求OC的最小值和OC达到最小值时△ABP的外接圆圆心M的坐标.
【答案】(1)详见解析;(2)点P的坐标为![]() ;(3)点M的坐标为
;(3)点M的坐标为![]() .
.
【解析】
(1)根据直径所对的圆周角等于90°及等角(或同角)的余角相等即可证明;
(2)先根据勾股定理求得AC的长,再证△OBP∽△ABC,根据相似三角形的对应边成比例列出比例式求解;
(3)记直线AC与y轴的交点为E,当OC最小时,OC⊥AE,根据解直角三角形和中点坐标公式求解即可.
(1)连结AC,
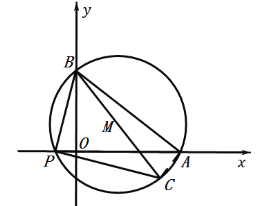
∵BC为![]() 的直径,
的直径,
∴∠BAC=∠BOP=90°
∵∠ACB=∠APB
∴∠OBP+∠APB=∠ABC+∠ACB=90°
∴∠OBP=∠ABC.
(2)∵∠BAC=90°, A(8,0)和B(0,6),
∴OB=6,OA=8,
∴AB=10
∴![]()
![]()
∵∠BAC=∠BOP=90°,∠OBP=∠ABC,
∴△OBP∽△ABC
∴![]() ,
,
∴![]()
![]() ,
,
∴点![]() 的坐标为
的坐标为![]()
(3)记直线AC与y轴的交点为E,
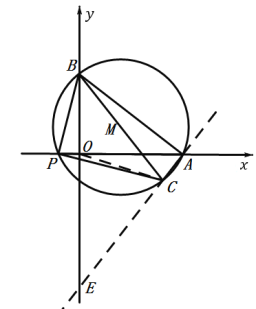
∵![]()
则∠OAE=∠OBA=90°-∠BAO
当OC最小时,OC⊥AE,
此时,OC=OA![]() sin∠OAE=OA
sin∠OAE=OA![]() sin∠OBA
sin∠OBA![]() ,
,
求得点C的坐标为![]()
又∵点M为BC的中点
∴![]() ,
,![]() ,
,
∴点M的坐标为![]() .
.

【题目】10月下旬,我校初三年级组织了体育期中测试.为了更好的了解孩子们的体育水平,全力备战中考,我校体育组从全年级体考成绩中随机抽查了20名男生和20名女生的体考成绩进行整理、描述和分析(成绩得分用x表示,共分成四组:A:47<x≤50,B:44<x≤47,C:41<x≤44,D:x≤41),下面给出了部分信息:20名男生的体考成绩(单位:分):50,46,50,50,47,49,39,46,49,46,46,43,49,47,40,48,44,42,45,44;20名女生的体考成绩为B等级的数据是:45,46,46,47,47,46,46.所抽取的学生体考成绩统计表
性别 | 平均数 | 中位数 | 众数 |
男 | 46 | 46 | b |
女 | 46.5 | c | 48 |
根据以上信息,解答下列问题:
(1)直接写出上述图表中a、b、c的值;
(2)根据以上数据,你认为我校男生的体育成绩好还是女生的体育成绩好?请说明理由(一条即可);
(3)我校初三年级共有2400名学生参与此次体考测试,估计参加测试的学生等级为A的有多少人?