题目内容
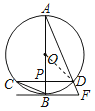
【题目】如图,AB为⊙O的直径,弦CD⊥AB,垂足为点P,直线BF与AD延长线交于点F,且∠AFB=∠ABC.

(1)求证:直线BF是⊙O的切线;
(2)若CD=2![]() ,BP=1,求⊙O的半径.
,BP=1,求⊙O的半径.
【答案】(1)见解析;(2)3
【解析】
(1)由圆周角定理得出∠ABC=∠ADC,由已知得出∠ADC=∠AFB,证出CD∥BF,得出AB⊥BF,即可得出结论;
(2)设⊙O的半径为r,连接OD.由垂径定理得出PD=PC=![]() CD=
CD=![]() ,得出OP=r-1在Rt△OPD中,由勾股定理得出方程,解方程即可.
,得出OP=r-1在Rt△OPD中,由勾股定理得出方程,解方程即可.
解:(1)证明:∵弧AC=弧AC,
∴∠ABC=∠ADC,
∵∠AFB=∠ABC,
∴∠ADC=∠AFB,
∴CD∥BF,
∵CD⊥AB,
∴AB⊥BF,
∵AB是圆的直径,
∴直线BF是⊙O的切线;
(2)解:设⊙O的半径为r,连接OD.如图所示:
∵AB⊥BF,CD=2![]() ,
,
∴PD=PC=![]() CD=
CD=![]() ,
,
∵BP=1,
∴OP=r﹣1
在Rt△OPD中,由勾股定理得:r2 =(r﹣1)2+(![]() )2
)2
解得:r=3.
即⊙O的半径为3.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目