题目内容
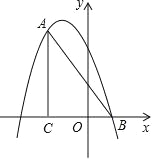
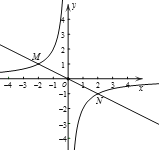
【题目】如图,反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象分别交于M,N两点,已知点M(-2,m).
的图象分别交于M,N两点,已知点M(-2,m).
(1)求反比例函数的表达式;
(2)点P为y轴上的一点,当∠MPN为直角时,直接写出点P的坐标.
【答案】(1)![]() ;(2)(0,
;(2)(0,![]() )或(0,
)或(0,![]() ).
).
【解析】
试题(1)把M(﹣2,m)代入函数式y=﹣![]() x中,求得m的值,从而求得M的坐标,代入y=
x中,求得m的值,从而求得M的坐标,代入y=![]() 可求出函数解析式;(2)根据M的坐标求得N的坐标,设P(0,m),根据勾股定理列出关于m的方程,解方程即可求得m进而求得P的坐标.
可求出函数解析式;(2)根据M的坐标求得N的坐标,设P(0,m),根据勾股定理列出关于m的方程,解方程即可求得m进而求得P的坐标.
试题解析:(1)∵点M(﹣2,m)在正比例函数y=﹣![]() x的图象上,
x的图象上,
∴m=﹣![]() ×(﹣2)=1,
×(﹣2)=1,
∴M(﹣2,1),
∵反比例函数y=![]() 的图象经过点M(﹣2,1),
的图象经过点M(﹣2,1),
∴k=﹣2×1=﹣2.
∴反比例函数的解析式为
(2)∵正比例函数y=﹣![]() x的图象与反比例函数y=
x的图象与反比例函数y=![]() 的图象分别交于M,N两点,点M(﹣2,1),
的图象分别交于M,N两点,点M(﹣2,1),
∴N(2,﹣1),
∵点P为y轴上的一点,
∴设P(0,m),
∵∠MPN为直角,
∴△MPN是直角三角形,
∴(0+2)2+(m﹣1)2+(0﹣2)2+(m+1)2=(2+2)2+(﹣1﹣1)2,
解得m=±![]()
∴点P的坐标为(0,![]() )或(0,﹣
)或(0,﹣![]() ).
).

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目