Question

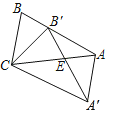
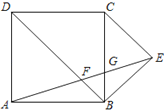
【题目】如图，四边形ABCD是正方形，以BC为底边向正方形外部作等腰直角三角形BCE，连接AE，分别交BD，BC于点F，G，则下列结论：①△AFB∽△ABE；②△ADF∽△GCE；③CG=3BG；④AF=EF，其中正确的有（ ）.

A.①③B.②④C.①②D.③④

Answer 1

【答案】B

【解析】

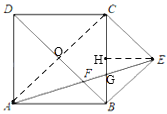
连接AC，交BD于O，过点E作EH⊥BC于H，由正方形的性质及等腰直角三角形的性质可得∠ADF=∠ABD=∠BCE=∠CBE=45°，可得∠ABE=135°，根据外角性质可得∠AFD=∠FAB+∠ABF>45°，利用平角定义可得∠AFB<135°，即可证明∠AFB≠∠ABE，可对①进行判断；由EH⊥BC可证明EH//AB，根据平行线的性质可得∠HEG=∠FAB，根据角的和差关系可证明∠DAF=∠CEG，即可证明△ADF∽△GCE；可对②进行判断，由EH//AB可得△HEG∽△BAG，根据相似三角形的性质即可得出BG=2HG，根据等腰直角三角形性质可得CH=BH，进而可得CG=2BG，可对③进行判断；根据正方形的性质可得OA=BE，∠AOF=∠FBE=90°，利用AAS可证明△AOF≌△EBF，可得AF=EF，可对④进行判断；综上即可得答案.

如图，连接AC，交BD于O，过点E作EH⊥BC于H，

∵ABCD是正方形，△BCE是等腰直角三角形，

∴∠ADF=∠ABD=∠BCE=∠CBE=45°，

∴∠ABE=135°，

∵∠AFD=∠BAF+∠ABF=∠BAF+45°>45°，

∴∠AFB=180°-∠AFD<135°，

∴∠AFB≠∠ABE，

∴△AFB与△ABE不相似，故①错误，

∵EH⊥BC，∠ABC=90°，

∴EH//AB，

∴∠HEG=∠FAB，

∴∠AFD=∠FAB+∠ABD=45°+∠HEG=∠CEG，

又∵∠ADB=∠GCE=45°，

∴△ADF∽△GCE，故②正确，

∵EH//AB，

∴△HEG∽△BAG，

∴,

∵△BCE是等腰直角三角形，

∴EH=CH=BH=BC=AB，

∴=，即BG=2HG，

∴CH=BH=3HG，

∴CG=CH+HG=4HG，

∴CG=2BG，故③错误，

∵ABCD是正方形，△BCE是等腰直角三角形，

∴∠AOF=90°，∠FBE=∠DBC+∠CBE=45°+45°=90°，OA=AB，BE=BC，

∴∠AOF=∠FBE，OA=BE，

在△AOF和△EBF中，，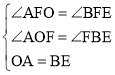

∴△AOF≌△EBF，

∴AF=EF，故④正确，

综上所述：正确的结论有②④，

故选：B.