题目内容
【题目】如图,已知平行四边形ABCD,∠ABC=120°,点E为线段BC上的动点,连接AE,将线段AE绕点A逆时针旋转60°得到线段AF,点E的对应点是点F,连接EF.
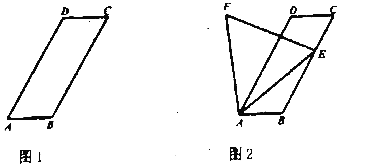
(1)当点E与点B重合时,在图1中将图补充完整,并求出∠CEF的度数;
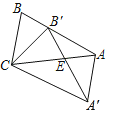
(2)如图2,求证:点F在∠ABC的平分线上.
【答案】(1)图见解析;60;(2)见解析
【解析】
(1)当点E与点B重合时,F点在AD上,根据题意画出图形后可得△AEF是等边三角形,即可求解;
(2)过F点作FG⊥AB交BA的延长线于G点,作FH⊥BC于H点,证△AFG≌△EFH,可得FG=FH,根据角平分线的判定定理即可得证.
(1)如图所示:平行四边形ABCD,∠ABC=120°,故∠A=60°,F点在AD上.
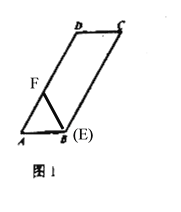
由旋转的性质可得:AE=AF,∠EAF=60°
∴△AEF为等边三角形
∴∠AEF=60°
∵∠ABC=120°
∴∠CEF=∠ABC-∠ABF=60°
(2)如图,过F点作FG⊥AB交BA的延长线于G点,作FH⊥BC于H点
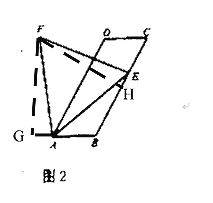
由(1)可得:△AEF是等边三角形
∴FA=FE,∠AFE=60°
∵FG⊥AB,FH⊥BC,∠ABC=120°
∴∠GFH=360°-90°-90°-120°=60°
∴∠GFH=∠AFE
∴∠GFH-∠AFH=∠AFE-∠AFH
即∠AFG=∠EFH
又∠FHE=∠FGA=90°,FA=FE
∴△AFG≌△EFH
∴FG=FH
又∵FG⊥AB,FH⊥BC
∴点F在∠ABC的平分线上.

练习册系列答案
相关题目