题目内容
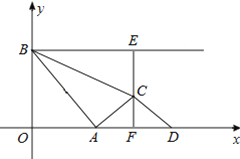
【题目】如图,点A是x轴正半轴上的动点,点B的坐标为(0,4),将线段AB的中点绕点A按顺时针方向旋转90°得点C,过点C作x轴的垂线,垂足为F,过点B作y轴的垂线与直线CF相交于点E,点D是点A关于直线CF的对称点,连接AC、BC、CD,设点A的横坐标为t.
(1)线段AB与AC的数量关系是 ,位置关系是 .
(2)当t=2时,求CF的长;
(3)当t为何值时,点C落在线段BD上?求出此时点C的坐标;
(4)设△BCE的面积为S,求S与t之间的函数关系式.
【答案】(1)AB=2AC,AB⊥AC;
(2)CF=1;
(3)当t=![]() ﹣2时,点C落在线段BD上;点C的坐标为(
﹣2时,点C落在线段BD上;点C的坐标为(![]() ,﹣1+
,﹣1+![]() );
);
(4)①当0<t≤8时, S=﹣![]() t2+
t2+![]() t+4;②当t>8时, S=
t+4;②当t>8时, S=![]() t2﹣
t2﹣![]() t﹣4;③t=8时,S=0.
t﹣4;③t=8时,S=0.
【解析】
(Ⅰ)根据“线段AB的中点绕点A按顺时针方向旋转90°得点C”推知AB与AC的关系;
(Ⅱ)由Rt△ACF∽Rt△BAO,得CF=![]() OA=
OA=![]() t,由此求出CF的值;
t,由此求出CF的值;
(Ⅲ)由Rt△ACF∽Rt△BAO,可以求得AF的长度;若点C落在线段BD上,则有△DCF∽△DBO,根据相似比例式列方程求出t的值;
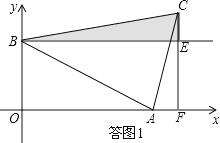
(Ⅳ)有三种情况,需要分类讨论:当0<t≤8时,如题图1所示;当t>8时,如答图1所示;t=8时.
(Ⅰ)∵如图,将线段AB的中点绕点A按顺时针方向旋转90°得点C,
∵AB=2AC,∠BAC=90°,
∴AB⊥AC.
(2)由题意,易证Rt△ACF∽Rt△BAO,
∴![]() .
.
∵AB=2AM=2AC,
∴CF=![]() OA=
OA=![]() t.
t.
当t=2时,CF=1;
(Ⅲ)由(1)知,Rt△ACF∽Rt△BAO,
∴![]() ,
,
∴AF=![]() OB=2,∴FD=AF=2,.
OB=2,∴FD=AF=2,.
∵点C落在线段BD上,
∴△DCF∽△DBO,
∴![]() ,
,
即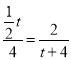 ,
,
整理 得t2+4t-16=0
解得 t=2![]() -2或t=-2
-2或t=-2![]() -2(不合题意,舍去)
-2(不合题意,舍去)
∴当t=2![]() -2时,点C落在线段BD上.
-2时,点C落在线段BD上.
此时,CF=![]() t=
t=![]() -1,
-1,
OF=t+2=2![]() ,
,
∴点C的坐标为(2![]() ,-1+
,-1+![]() );
);
(Ⅳ)①当0<t≤8时,如题图1所示:
S=![]() BECE=
BECE=![]() (t+2)(4-
(t+2)(4-![]() t)=-
t)=-![]() t2+
t2+![]() t+4;
t+4;
②当t>8时,如答图1所示:CE=CF-EF=![]() t-4
t-4
S=![]() BECE=
BECE=![]() (t+2)(
(t+2)(![]() t-4)=
t-4)=![]() t2-
t2-![]() t-4;
t-4;
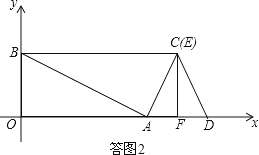
③如答图2,当点C与点E重合时,CF=OB=4,可得t=OA=8,此时S=0.