题目内容
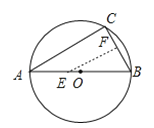
【题目】如图,AB是⊙O的直径,弦BC=4cm,F是弦BC的中点,∠ABC=60°.若动点E以2cm/s的速度从A点出发沿着A→B→A的方向运动,设运动时间为t(s)(0≤t<6),连接EF,当△BEF是直角三角形时,t的值为___________________.
【答案】2或![]() 或
或![]() .
.
【解析】
求出E移动的路程是0≤s<12,求出∠C=90°,求出AB,分为三种情况:画出图形,根据图形求出移动的距离即可.
解:解:∵0≤t<6,动点E以2cm/s的速度从A点出发沿着A→B→A的方向运动,
∴E运动的距离小于12cm,设E运动的距离是scm,
则0≤s<12,
∵AB是⊙O直径,
∴∠C=90°,
∵F为BC中点,BC=4cm,
∴BF=CF=2cm,
∵∠C=90°,∠B=60°,
∴∠A=30°,
∴AB=2BC=8cm,
分为三种情况:
①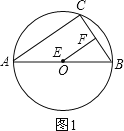
当∠EFB=90°时,
∵∠C=90°,
∴∠EFB=∠C,
∴AC∥EF,
∵FC=BF,
∴AE=BE,即E和O重合,AE=4,
t=4÷2=2(s);
②
当∠FEB=90°时,∵∠ABC=60°,
∴∠BFE=30°,
![]()
AE=8-1=7,
![]()
③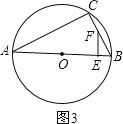
当到达B后再返回到E时,∠FEB=90°,
此时移动的距离是8+1=9,
![]()
故答案为1或![]() 或
或![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200-2x | |
已知该商品的进价为每件30元,设销售该商品的每天利润为y元[
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.