Question

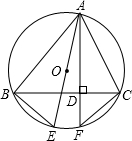
如图，⊙O为△ABC的外接圆，弦CD平分∠ACB，∠ACB=90°，求证：CA+CB=

2

CD．

Answer 1

证明：连接AD，BD，过A作AM⊥CD，过B作BN⊥CD，垂足分别为M、N，
∵AB为直径，CD平分∠ACB交⊙O于D，
∴∠ACD=∠BCD=

1

2

∠ACB=45°，
∴△ACM与△BCN都是等腰直角三角形，AD=BD，
在Rt△ACM中，CM=

2

2

CA，在Rt△BCN中，CN=

2

2

CB，
∴CM+CN=

2

2

（CA+CB），
∵AB是直径，
∴∠ADB=90°，
∴∠ADM+∠BDN=90°，
又∵∠BDN+∠DBN=90°，
∴∠ADM=∠DBN，
在△ADM与△BDN中，

∠ADM=∠DBN ∠AMD=∠DNB=90° AD=BD

，
∴△ADM≌△BDN（AAS），
∴DN=AM，
又∵AM=CM（等腰直角三角形两直角边相等），
∴CM=DN，
∴CD=CN+DN=CN+CM=

2

2

（CA+CB），
∴CA+CB=

2

CD．