题目内容
如图,AB、AC是⊙O的弦,AD⊥BC于点D,交⊙O于点F,AE是⊙O的直径,试判断弦BE与弦CF的大小关系,并说明理由.
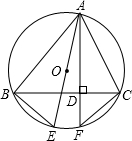

BE=CF,
理由:
∵AE为⊙O的直径,AD⊥BC
∴∠ABE=90°=∠ADC
∵∠AEB=∠ACB(同弧所对的圆周角相等),
∴∠BAE=∠CAF(等角的余角相等)
∴
=
,
∴BE=CF.
理由:
∵AE为⊙O的直径,AD⊥BC
∴∠ABE=90°=∠ADC
∵∠AEB=∠ACB(同弧所对的圆周角相等),
∴∠BAE=∠CAF(等角的余角相等)
∴
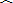 |
| BE |
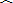 |
| CF |
∴BE=CF.

练习册系列答案
相关题目