Question

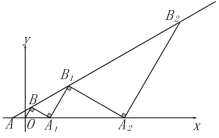
【题目】在直角坐标系中，如图所示，把∠BAO放在直角坐标系中，使射线AO与x轴重合，已知BAO=30°，OA=OB=1，过点B作BA1⊥OB交x轴于A1，过点A1做B1A1⊥BA1交直线AB于点B1，过B1作B1A2⊥B1A1交x轴于点A2，再过A2依次作垂直…．则△A6B6A7的面积为_____.

Answer 1

【答案】．

【解析】

根据OA的长即可求出A的坐标，根据OB和∠BOA1=60°，即可求出B的坐标，设直线AB的解析式是y=kx+b，把A、B的坐标代入得出方程组，求出方程组的解；推出∠BAC=∠ABO=30°，求出∠BOC=60°，∠BA1O=30°，求出BA1=，求出A1B1=×、B1A2=3=××，同理求出A6B6=12个相乘，B6A7=13个相乘，根据三角形的面积公式求出即可．

∵OA=1，

∴A（-1，0），

易求B（，）．

设直线AB的解析式是：y=kx+b，

把A（-1，0），B（，）代入得：

，

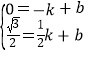解得：，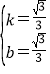

∴直线AB的解析式为：y=x+．

∵OB=OA=1，

∴∠BAC=∠ABO=30°，

∴∠BOC=60°，

∴∠BA1O=30°，

∴BA1=，

同理∠BB1A1=30°，

∴B1A1=3=×，

同理：B1A2=3=××，

…

A6B6=××…×（12个相乘），

B6A7=××…×（13个相乘），

∴△A6B6A7的面积是：A6B6×B6A7=×（××…×）×（××…×）

=，

答：△A6B6A7的面积是．