题目内容
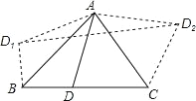
【题目】如图，在△ABC中，∠ABC=45°，∠ACB=60°，BC=2
+2，D是BC边上异于点B，C的一动点，将三角形ABD沿AB翻折得到△ABD1，将△ACD沿AC翻折得到△ACD2，连接D1D2，则四边形D1BCD2的面积的最大值是_____.
【答案】9+4
．
【解析】
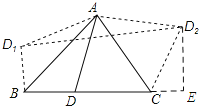
如图所示：过点D2作D2E⊥BC，垂足为E．设DC=x，则BD=2+2-x．然后根据四边形D1BCD2的面积等于梯形D1BED2的面积减去三角形CED2的面积列函数关系是求解即可．
如图所示：过点D2作D2E⊥BC，垂足为E．
设DC=x，则BD=2+2-x．
由翻折的性质可知：∠D1BD=90°，∠ECD2=60°，D1B=BD=2+2-x，CD2=DC=x．
∵在Rt△CED2中，∠ECD2=60°
∴EC=
x，D2E=
x．
∴SD1BCD2=SD1BED2-S△CED2
=（D1B+D2E）BE-×CE×ED2
=×（2+2-x+x）（2+2+x）-×x×x
=
（x-2）2+9+4．
∴当x=2时，四边形D1BCD2的面积有最大值，最大值为9+4．
故答案为：9+4．
练习册系列答案
相关题目
