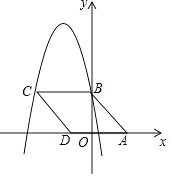题目内容
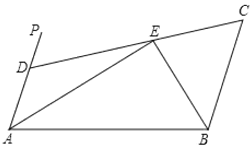
【题目】如图,在平行四边形ABCD的纸片中,AC⊥AB,AC与BD交于O,将△ABC沿对角线AC翻折得到![]() .
.
(1)求证:四边形ACDB’是矩形.
(2)若平行四边形ABCD的面积为12,求翻折后纸片重叠部分的面积,即![]() .
.

【答案】(1)见解析;(2)3
【解析】
(1)根据平行四边形的性质以及已知条件求证出四边形ACDB'是平行四边形,进而得出四边形ACDB'是矩形;
(2)根据矩形的性质以及平行四边形的性质求出△ACD的面积,因为△AEC和△EDC可以看作是等底等高的三角形,即可得出结论.
(1)∵四边形ABCD是平行四边形,∴AB平行且等于CD.
∵△AB'C是由△ABC翻折得到的,AB⊥AC,∴AB=AB',点A、B、B'在同一条直线上,∴AB'∥CD,∴四边形ACDB'是平行四边形.
∵B'C=BC=AD,∴四边形ACDB'是矩形.
(2)∵四边形ACDB'是矩形,∴AE=DE.
∵SABCD=12cm2,∴S△ACD=6cm2,∴S△AEC![]() S△ACD=3cm2.
S△ACD=3cm2.

练习册系列答案
相关题目