题目内容
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为A(1,0)、B(3,0).抛物线y=x2﹣2mx+m2﹣4的顶点为P,与y轴的交点为Q.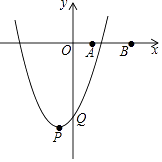
(1)填空:点P的坐标为;点Q的坐标为(均用含m的代数式表示)
(2)当抛物线经过点A时,求点Q的坐标.
(3)连接QA、QB,设△QAB的面积为S,当抛物线与线段AB有公共点时,求S与m之间的函数关系式.
(4)点P、Q不重合时,以PQ为边作正方形PQMN(P、Q、M、N分别按顺时针方向排列).当正方形PQMN的四个顶点中,位于x轴两侧或y轴两侧的顶点个数相同时,直接写出此时m的取值范围.
【答案】
(1)(m,﹣4),(0,m2﹣4)
(2)解:将A(1,0)代入y=x2﹣2mx+m2﹣4中,
得到1﹣2m+m2﹣4=0,
解得m=﹣1或3,
当m=﹣1时,m2﹣4=﹣3,点Q的坐标为(0,﹣3),
当m=3时,m2﹣4=5,点Q的坐标为(0,5).
(3)解:如图1中,
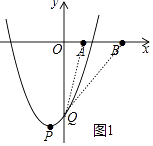
由题意 ![]() ,解得﹣1≤m≤1,
,解得﹣1≤m≤1,
∴当﹣1≤m<≤时,S= ![]() ABOQ=
ABOQ= ![]() 2(4﹣m2)=4﹣m2.
2(4﹣m2)=4﹣m2.
如图2中,
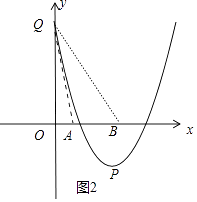
由题意 ![]() ,解得3≤m≤5,
,解得3≤m≤5,
当3≤m≤5时,S= ![]() ABOQ=m2﹣4.
ABOQ=m2﹣4.
(4)解:如图3中,如图当点N在y轴上时,满足条件,易知m2﹣4=﹣3,解得m=﹣1或1(舍弃).
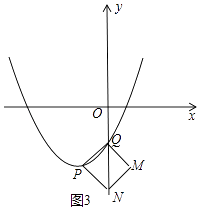
如图4中,作ME⊥y轴于E,PF⊥y轴于F.
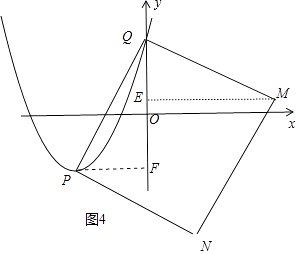
由△MEQ≌△QFP,可得QE=PF=﹣m,可得点M的纵坐标为m2﹣4+m,
当m2+m﹣4>0时,满足条件,
解得m< ![]() 或m>
或m> ![]() (舍弃)
(舍弃)
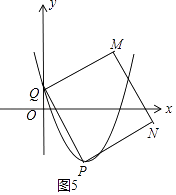
如图5中,同法可得, ![]() 时满足条件,解得2<m<4.
时满足条件,解得2<m<4.
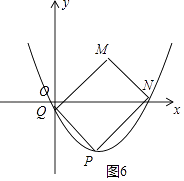
如图6中,同法可得 ![]() 时满足条件,此不等式无解.
时满足条件,此不等式无解.
综上所述,满足条件的m的范围是m< ![]() 或m=﹣1或2<m<4.
或m=﹣1或2<m<4.
【解析】解:(1)∵y=x2﹣2mx+m2﹣4=(x﹣m)2﹣4,
∴顶点P(m,﹣4),
令x=0,得到y=m2﹣4,
∴Q(0,m2﹣4).
所以答案是(m,﹣4),(0,m2﹣4).