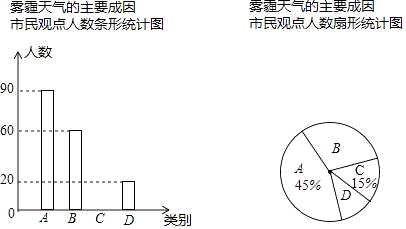
题目内容
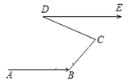
【题目】“浏阳河弯过九道弯,五十里水路到湘江.”如图所示,某段河水流经 B,C,D 三点拐弯后与原来流向相同,若∠ABC =6∠CDE,∠BCD =4∠CDE,则∠CDE= _________.
【答案】![]()
【解析】
由题意可得AB∥DE,过点C作CF∥AB,则CF∥DE,由平行线的性质可得,∠BCF+∠ABC=180°,所以能用∠CDE表示出∠BCF,再由CF∥DE,所以∠CDE=∠DCF,利用∠BCD =∠BCF+∠DCF =4∠CDE,从而求得∠CDE.
解:由题意得,AB∥DE, 过点C作CF∥AB,则CF∥DE,
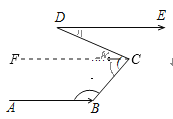
∴∠BCF+∠ABC=180°,
又∵∠ABC =6∠CDE
∴∠BCF=180°-6∠CDE,
∵∠CDE=∠DCF,
∴∠BCD=∠BCF+∠DCF=180°-6∠CDE+∠CDE=180°-5∠CDE,
而∠BCD =4∠CDE,
∴4∠CDE=180°-5∠CDE,
∴∠CDE=20°
故答案为:20°.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目